Pagina Precedente

Corso di

          FISICA GENERALE

Docente:

          Prof. Andrea Mura

 

Testo consigliato:

          D. Halliday, R. Resnick, J. Walzer

       Fondamenti di Fisica:

       Meccanica e Termologia

          VI Edizione Editrice Ambrosiana

          P.A. Tipler G. Mosca

       Corso di Fisica

       Meccanica Onde e Termodinamica

          IV Edizione Editrice  Zanichelli

 

Orario di ricevimento:

          Mercoledì h 11.00-12.00

          Dipartimento di Fisica

          Cittadella Universitaria di Monserrato

 

         

 

 

Programma del corso di Fisica Generale

Architettura

Durata del corso: 60 ore

Nozioni introduttive
Misure. Il sistema Internazionale delle unità di misura. Cambiamento di unità. Lunghezza. Tempo. Massa.
Cinematica
Il moto. Posizione e spostamento. Velocità media. Velocità Istantanea. Accelerazione. Accelerazione costante, Moto uniformemente accelerato. Accelerazione nel moto di caduta libera. Estensione al caso bidimensionale. Moto di proiettili. Moto circolare uniforme: velocità angolare, accelerazione centripeta. Moto relativo in due dimensioni
Dinamica
Le cause della accelerazione dei corpi. Prima legge di Newton. La Forza. La Massa. Seconda legge di Newton. Forze Particolari. Terza legge di Newton. Attrito e sue proprietà. Resistenza del mezzo e velocità limite. Dinamica del moto circolare uniforme. Energia cinetica. Il lavoro. Lavoro ed energia cinetica. Lavoro della forza peso. Lavoro svolto dalle forze variabili. Lavoro svolto da una molla. Potenza. Energia potenziale. Influenza del cammino per le forze conservative. Determinazione della energia potenziale. Energia meccanica e sua conservazione. Curve della energia potenziale. Conservazione della energia. Il centro di massa. Seconda legge di Newton per un sistemi di punti materiali. Quantità di moto. Quantità di moto per un sistema di punti materiali. Conservazione della quantità di moto. Variabili rotazionali. Quantità angolari e vettori. Rotazione con accelerazione angolare costante. Variabili angolari e lineari. Energia cinetica di rotazione. Calcolo del momento di inerzia. Momento di una forza. Seconda legge di Newton per il moto rotatorio. Rotolamento. Momento angolare. Seconda legge di Newton in forma angolare. Momento angolare di un sistema di particelle. Momento angolare di un corpo rigido che ruota attorno ad un asse fisso. Conservazione del momento angolare. Equilibrio e suoi requisiti. Centro di gravità. Esempi di equilibrio statico.
Fluidi
Definizione di fluido. Densità e pressione. Fluidi a riposo. Misura della pressione. Principio di Pascal. Principio di Archimede. Legge di Stevino. Fluidi ideali in movimento. Linee di flusso ed equazione di continuità. Equazione di Bernoulli.
Termodinamica
La termodinamica, Legge zero della termodinamica. Misura della temperatura. Le scale termometriche. Dilatazione termica. Temperatura e calore.

Assorbimento del calore da parte dei solidi e liquidi. Calore e lavoro. Prima legge della termodinamica. Casi particolari della prima legge della termodinamica. Trasmissione del calore. Gas reali e ideali. Pressione, temperatura e velocità quadratica media nei gas ideali. Energia cinetica di traslazione. Calori specifici molari per i gas ideali. Gradi di libertà e calore specifico molare. Espansione adiabatica di un gas ideale. Trasformazioni reversibili e irreversibili. Macchine termiche e Secondo Principio. Frigoriferi e Secondo Principio. Ciclo di Carnot, Scala termodinamica della temperatura. Entropia e trasformazioni reversibili. Entropia e trasformazioni irreversibili. Entropia e Secondo Principio

 

.

Esercitazione n°1 di Fisica Generale

Cinematica (25-03-2011)

 

1) 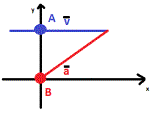   Una particella A si muove parallelamente all’asse positivo delle x lungo la linea y = 30 m con velocità costante e in modulo uguale a v = 3.0 m/s. Nello stesso istante in cui essa passa per l’asse y una particella B parte dall’origine con velocità nulla, accelerazione costante e modulo a = 0.40 m/s2.

a)    Qual è l’angolo J fra l’accelerazione e l’asse y nel momento della collisione tra le due particelle?

 

2)    Un sasso viene lanciato verso l’alto con velocità di 42 km/h. Potendo trascurare ogni resistenza dell’aria:

a)    quanto tempo impiegherà a ricadere a terra?

b)    Quale sarà la massima altezza raggiunta?

 

 

3)    Un giocatore di calcio colpisce il pallone in modo da imprimergli una velocità iniziale di 15.5 m/s inclinata di 36° rispetto all’orizzontale; determinare:

a) 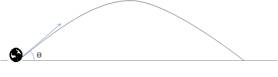   Il tempo impiegato dal pallone a raggiungere il punto più alto della traiettoria,

b)    La sua massima altezza,

c)    La sua gittata e il tempo di volo,

d)    La velocità con la quale tocca il suolo.

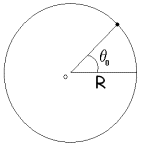
4)    Un punto sul bordo di una ruota di diametro 2,25 m cambia gradualmente velocità da 18 m/s a 32 m/s in 9.2 secondi.

a)    Qual è l’accelerazione tangenziale della ruota durante questo intervallo di tempo?

b)   Qual è l’accelerazione radiale della ruota?

 

 

 

Esercitazione n°2 di Fisica Generale

Dinamica

 

1) 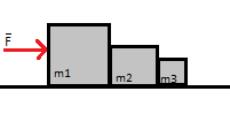     Il sistema di tre casse mostrato in figura è soggetto alla forza F = 187.0 N e si sposta sulla superficie orizzontale priva di attrito con accelerazione a = 1.46 m/s2. Sapendo che m1 = 51.4 kg ed m3 = 33.7 kg, si calcolino:

a)      La massa m2;

b)      Le forze esercitate da m1 su m2;

c)      Le forze esercitate da m2  su m3.

 

 

 

2)      Tre blocchi sono collegati come mostrato in figura e trascinati su un piano orizzontale privo di attrito da una forza F che imprime al sistema l’accelerazione a = 1.2 m/s2. Supposto che m1 = 3.9 kg, m2 = 2.6 kg, m3 = 2.6 kg  si calcolino:

a)      La forza F;

b)      La tensione T1;

c)      La tensione T2.

 

 

 

 

3) 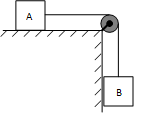    Un blocco di massa 5 kg è posto su una superficie orizzontale liscia ed è tirato da una fune attaccata a un blocco di massa 8 kg sospeso a una puleggia che ha soltanto lo scopo di cambiare la direzione della tensione della fune.

a)       Calcolare l’accelerazione del sistema

b)       Calcolare la tensione della fune

 

 

 

 

 

 

 

4)      Un ragazzo scivola su una lastra di ghiaccio per 15 m prima di fermarsi. Se la sua velocità iniziale era 6.0 m/s, quale è il coefficiente di attrito tra il ragazzo e il ghiaccio?

 

 

5)      Un armadio del peso di 310 N è appoggiato sul pavimento. I coefficienti di attrito statico e dinamico fra armadio e pavimento sono rispettivamente 0.38 e 0.25.

a)      Con quale forza minima orizzontale si riuscirà a metterlo in movimento?

b)      Quale componente orizzontale dovrà avere la forza capace di tenerlo in movimento, a velocità costante?

c)      Se si continuasse a spingere con la forza richiesta per iniziare il moto quale sarebbe l’accelerazione dell’armadio?

 

 

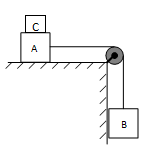
6)     I blocchi A e B pesano rispettivamente 44 N e 22 N.

a)     Trovare il peso minimo del blocco C da collocare su A per impedirne lo slittamento, sapendo che il coefficiente di attrito statico del piano è 0.2.

b)     Rimuovendo il blocco C, se il coefficiente di attrito dinamico del piano è 0.15, quanto vale il modulo dell’accelerazione iniziale della cassa?

 

 

 

 

 

 

ESERCITAZIONE 3

 

 

1)     Un uomo di 70 kg e una slitta sono sulla superficie di un lago ghiacciato, alla distanza di 18 m l’uno dall’altra. Tirando la slitta a sé con una corda, l’uomo esercita sulla slitta una forza F di 5.6 N. Supponendo nulli gli attriti, se la forza rimane costante:

a)     A che distanza dalla posizione iniziale dell’uomo si incontrano?

b)     Qual è il lavoro fatto dalla forza F durante tale spostamento?

 

2) 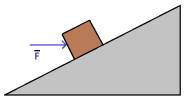    forza5.pngUna forza orizzontale F spinge una cassa di massa 48 kg lungo un piano inclinato di 32° rispetto all’orizzontale e privo di attrito. Se la cassa si muove con velocità costante, calcolare:

a)     La forza F;

b)     Il lavoro fatto dalla forza F per spostare la cassa di 5 m.

 

3) 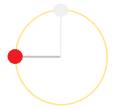    forza6.pngUna palla di massa m = 25 g è solidale  a una estremità di una sbarretta leggera di lunghezza L = 50  cm vincolata all’altra estremità. La palla può quindi muoversi su una circonferenza disposta verticalmente. Inizialmente la sbarretta è posta orizzontalmente e riceve una spinta verso il basso in modo da arrivare a fermarsi nella posizione verticale.

a)     Quale è l’energia potenziale della pallina nella posizione  verticale?

b)     Quale velocità iniziale è stata data alla palla?

 

4) 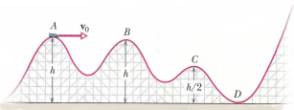    Un carrello da montagne russe parte dal punto a della figura con una velocità v0= 12 m/s. Se h = 8 m quanto vale il modulo della velocità del carrello:

a)     Nel punto B;

b)     Nel punto C;

c)      Nel punto D.

Si consideri il carrello come un punto materiale sempre aderente alle rotaie.

 

5)     Una pietra di 7.94 kg è ferma sopra una molla compressa di 10.2 cm. Si determini:

a)     La costante elastica della molla;

b)     La pietra viene spinta verso il basso di altri 28.6 cm e quindi è lasciata andare. Quanta energia potenziale  viene immagazzinata dalla molla poco prima del rilascio della pietra?

 

 

ESERCITAZIONE 4

 

 

 

 

 

 

1)     Una ruota gira liberamente intorno a un albero, avente momento d’inerzia trascurabile, alla velocità angolare di 800 giri/min. Un’altra ruota, inizialmente a riposo, avente momento d’inerzia doppio della prima, è accoppiata d’improvviso allo stesso albero.

a)      Qual è la velocità angolare del sistema risultante albero + due ruote?

 

 

 

 

 

 

 

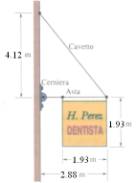
2)     Un’insegna omogenea quadrata di lato 1.93 m e massa 52.3 kg, è appeso ad una sbarra orizzontale di massa trascurabile e lunga L = 2.88 m. Come è illustrato in figura, un’estremità della sbarra è fissata a una parete verticale mentre l’altra è attaccata a un cavo. Il cavo ha un’estremità fissata alla parete in un punto situato 4.12 m sopra quello in cui è fissata la sbarra.

a)     Determinare la tensione del cavo

b)     Calcolare le componenti orizzontale e verticale della forza esercitata dalla parete sulla sbarra.

 

 

 

 

 

 

 

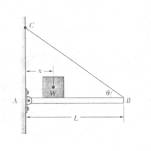
3)     Una sottile barra orizzontale AB di lunghezza L e massa trascurabile è incernierata a una parete verticale e sostenuta in B da un filo sottile BC che forma un angolo q con il piano orizzontale. Un peso W può essere spostato lungo la barra in qualunque posizione. Chiamiamo x la distanza dalla parete del suo centro di gravità. Trovare, in funzione di x:

b)      La tensione del filo

c)      La componente orizzontale della forza esercitata sulla barra dal perno in A

d)      La componente verticale della forza esercitata sulla barra dal perno in A

 

tmp

 

 

 

 

 

 

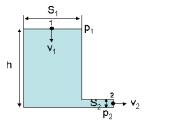
4) In un grande serbatoio d’acqua la superficie libera è a 3.68 m da terra. Nella parte bassa del serbatoio, a 1.15 m da terra, c’e’ un tubo orizzontale, di sezione costante e molto più piccola della sezione del serbatoio, la cui  apertura è chiusa con un tappo.

a)      Qual è la pressione sul fondo del serbatoio?

b)      Qual è la velocità con cui l’acqua esce dall’apertura se si toglie il tappo? 

 

 

 

 

 

 

 

ESERCITAZIONE 5