Pagina Precedente
Esercitazione n°1 di Fisica 1 (18 -03 -2013)
Esercizio 1
Un aeroplano percorre 129,8 km in linea retta verso nord-est formando un angolo di 22,5° con la direzione sud-nord. Quanto si e’ allontanato nella direzione nord e nella direzione est l’aeroplano dal punto di partenza?
Esercizio 2
Un automobile viaggia per 31,2 km verso est, poi svolta verso nord e viaggia per 41,3 km prima di fermarsi.
a) Quale sarà lo spostamento risultante dell’automobile?
Esercizio 3
Un punto materiale si muove con accelerazione costante pari a 5,2 cm/s2 , all’istante iniziale ha una velocità di 10,4 m/s.
a) Si determini la velocità dopo mezz’ora.
Esercizio 4
Un automobile viaggia verso nord e la sua velocità si riduce uniformemente da 55,4 km/h a 29,7 km/h in una distanza di 100,2 m.
a) Determinare il modulo e la direzione dell’accelerazione.
b) Quanto tempo e’ trascorso durante questa decelerazione?
Esercizio 5
Si lascia cadere una pietra da una finestra posta a 39,9 m dal suolo.
a) Quanto tempo impiegherà per raggiungere il suolo?
b) Qual e’ la velocità della pietra quando raggiungere il suolo?
Esercizio 6
Un lanciatore di baseball scaglia la palla verticalmente lungo l’asse y con velocità iniziale 12,2 m/s
a) Quanto tempo impiega la palla per raggiungere il punto più alto della sua traiettoria?
b) A che altezza arriva rispetto al punto di partenza?
c) Quanto tempo impiegherà la palla per raggiungere un punto situato a 5,2 m sopra il punto di partenza?
Esercizio 7
Un giocatore di pallone colpisce una palla ad un angolo di 30,20 con l’orizzontale con una velocità iniziale di 19,8 m/s. Supponendo che la palla si muova in un piano verticale:
a) Determinare l’istante in cui la palla raggiunge il punto più alto della sua traiettoria.
b) Qual e’ l’altezza massima raggiunta dalla palla?
c) Qual e’ lo spostamento orizzontale della palla?
d) Per quanto tempo la palla rimane in aria?
e) Qual e’ la velocità della palla quando raggiunge il suolo?
Esercizio 8
La luna gira attorno alla terra facendo un giro completo in 27,3 giorni. Si assuma che l’orbita sia circolare e abbia un raggio di 385000 km.
a) Qual’e’ il modulo dell’accelerazione della luna verso la terra?
Esercitazione n°2 di Fisica 1
Esercizio 1
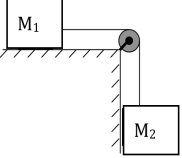Un blocco scorrevole di massa M1,
è libero di muoversi lungo una superficie orizzontale liscia priva di attrito.
Il blocco scorrevole è legato mediante una fune che passa su una puleggia priva
di massa e di attrito, a un secondo blocco appeso di massa M2.
Mentre il blocco appeso cade, il blocco scorrevole subirà un’accelerazione
verso destra. Supposto che M1= 2,5kg M2= 1,5 kg, calcolare: a) l’accelerazione del blocco, b)
la tensione della fune.
Esercizio 2
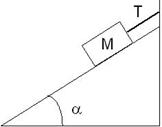
Un blocco di massa 12,5 kg è trattenuto da una fune su un piano liscio, inclinato di un angolo a = 30,6o , calcolare:
a) i moduli della forza T applicata al blocco dalla corda e della forza FN applicata al blocco dal piano.
b) l’accelerazione subita dal blocco che scivola giù una
volta che si è tagliata la fune.
Esercizio 3
Un blocco di massa m
= 0,49 kg scivola con una velocità costante v di 0,58 m/s, su un
piano orizzontale privo di attrito di un tavolo. Il blocco si arresta
comprimendo una molla collocata sul suo percorso. La costante elastica della
molla è k=759 N/m. Per quale distanza massima d è compressa la molla?
Esercizio 4
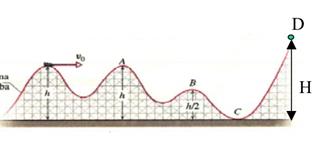
Un carrello di massa m = 23,8 kg viene lanciato con velocità v0=24,9 m/s dalla prima gobba delle montagne russe che si trova ad una altezza h = 26,4 m dal suolo. Se la rotaia è priva di attrito, calcolare: a) con quale velocità arriva nel punto A , B, C; b) a quale altezza H si ferma nel
punto D?
Esercitazione n°3 di Fisica 1
Esercizio 1
Un blocco di 5,2 kg parte da fermo dalla sommità di un piano inclinato di 35,2o e scorre giù per il piano inclinato per una distanza di 2,5 m in 2,4 s. Determinare:
a) l’accelerazione del blocco, b) la forza di attrito agente sul blocco.
Esercizio 2
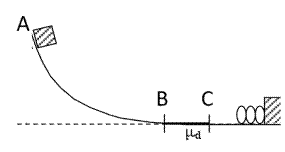Un blocco di 9,8 kg e’
lasciato libero in un punto A di una pista posto ad altezza pari a 4,2 metri.
La pista e’ priva di attrito, fatta eccezione per il
tratto BC, lungo 5,9 m. Il blocco scende lungo la pista e colpisce una molla di
costante elastica k= 2280 N/m e la comprime di 0,3 m. Determinare il
coefficiente d’ attrito dinamico nel tratto BC tra pista e blocco.
Esercizio 3
Un blocco di 50,2 kg inizialmente fermo viene spinto per 6,2 m lungo un pavimento orizzontale scabro con una forza costante orizzontale di 128,3 N. Il coefficiente di attrito tra blocco e pavimento e’ 0,4. Determinare a) il lavoro compiuto dalla forza applicata e dalla forza di gravità, b) la variazione di energia cinetica del blocco c) la velocità finale della cassa.
Esercizio 4
La cabina di un ascensore di massa m= 490 kg
sta scendendo con velocità v1
=4,0 m/s, quando il sistema di argani che ne controlla la discesa comincia a
slittare, lasciandola slittare con un’accelerazione costante a= g/6.
a)
Durante la sua caduta per una distanza d=11 m, qual e’
il lavoro sviluppato sulla cabina dalla forza gravitazionale? b) Durante la
caduta di 11 m qual e’ stato il lavoro sviluppato
sulla cabina dalla forza di trazione T
diretta verso l’alto esercitata dal cavo dell’ascensore? c) Qual e’ il lavoro totale sviluppato sulla cabina durante la
caduta di 11 m? d) Qual e’ l’energia cinetica della
cabina alla fine della caduta di 11 m?
Esercizio 5
La cabina di un montacarichi a pieno carico ha
una massa complessiva di 1150 kg e deve salire di 53,5 m in 3,2 min. Il
contrappeso ha una massa di 900 kg. Determinare la potenza richiesta al motore
quando il cavo solleva la cabina, supponendo che viaggi a velocità costante.
Esercitazione n°4 di Fisica 1 (16 aprile )
Esercizio 1
Una trave omogenea è incernierata a un muro. Un cavo connesso al muro a una distanza d = 6,0 m sopra il cardine è attaccato all’ altro estremo della trave. La trave forma un angolo di 30° con l’orizzontale, quando un blocco di massa m = 5,2 kg è appeso con una corda all’estremo non incernierato della trave. Se la trave ha massa M = 30 kg e lunghezza l = 10 m, calcolare: a) la tensione del cavo e b) le forze vinvolari esercitate dal cardine sulla trave.
Esercizio 2
Una scala uniforme di lunghezza L=5,6 m pesa 12 N ed è poggiata contro una parete verticale priva di attrito. Il piede della scala si trova a una distanza d=3,6 m dalla parete. Qual’e’ il minimo coefficiente di attrito tra la scala e il pavimento, che impedisce alla scala di slittare?
Esercizio 3
Due blocchi di massa m1 = 15,1 kg e m2 = 20,1 kg, sono collegati da una fune, di massa trascurabile, che passa su una carrucola di 0,25 m di raggio e momento d’inerzia I. Il blocco di massa m1, posto su un piano inclinato di 37,10 , si muove con un accelerazione costante di 2,1 m/s2. Determinare la tensione T1 nel primo tratto della fune e il momento d’ inerzia della carrucola.
Esercizio 4
Un blocco di massa m=679 g, fissato a una molla con k=65 N/m, e’ trascinato a una distanza x=11,1 cm dalla sua posizione di equilibrio x=0 su una superficie priva di attrito, e lasciato libero, da fermo, all’istante t=0. Quali sono la pulsazione, la frequenza e il periodo dell’oscillazione risultante? Qual’e’ l’ampiezza dell’oscillazione? Qual e’ la massima velocità del blocco oscillante? Qual e’ la funzione spostamento x(t) del sistema blocco molla?
Esercizio 5
Un blocco di massa m=680 g, fissato a una molla con k=65 N/m, e’ trascinato a una distanza x=11 cm dalla sua posizione di equilibrio x=0 su una superficie priva di attrito, e lasciato libero, da fermo, all’istante t=0.
Qual e’ l’energia meccanica E
dell’oscillatore? Quali sono l’energia potenziale e l’energia cinetica
dell’oscillatore quando la particella e’ a metà
strada verso il massimo spostamento?
Esercizio 6
Una corda tesa ha una massa per unità di lunghezza di 4,9 g/cm e una tensione di 9,8 N. Un’onda sinusoidale si muove su questa corda con un’ampiezza di 0,1 mm e una frequenza di 99,2 Hz ed e’ in moto nel verso in cui diminuisce x. Calcolare: la velocità dell’onda, il numero d’onda angolare k; la pulsazione w.
Esercizio 7
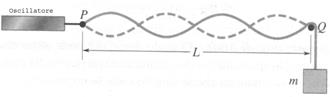
Una corda legata in P a un oscillatore sinusoidale e passante al di sopra di un supporto in Q è tesa da un blocco di massa m. La distanza L tra P e Q è 1,2 m, la densità di massa della corda è µ = 1,6 g/m. L’ampiezza del movimento in P è abbastanza piccola da poter considerare questo punto un nodo. Un nodo esiste anche in Q. Se la massa vale 846 g, determinare: la velocità dell’onda sulla corda tesa e la frequenza che deve avere l’oscillatore affinché sulla corda si instauri la quarta armonica.
Esercitazione n°5 di Fisica 1
Esercizio 1
Un blocco di rame di 80 g, preso da una fornace, viene posto in un contenitore di vetro da 320 g contenente 220 g di acqua. Si osserva un aumento della temperatura dell’acqua da 13 a 28 oC. Qual’era, approssimativamente, la temperatura della fornace?
Esercizio 2
Un blocco di massa m= 1,2 Kg dopo aver assorbito una quantità di calore pari a 130 J varia la sua temperatura di 12 oC. Calcolare a) il calore specifico e b) la capacità termica del corpo.
Esercizio 3
Una sbarra di alluminio ha una lunghezza di 10 cm alla temperatura di 10 oC. Di quanto si allunga alla temperatura di 40 oC?
Esercizio 4
Una parete e’ costituita da una tavola di pino per uno spessore di la e mattoni per uno spessore ld ,’ pari a 2,2 la. Tali strati racchiudono due strati di materiale non noto di spessore identico e uguale conducibilità termica. La conducibilità del pino e’ ka e quella dei mattoni e’ kd (= 5,2 ka). L’area superficiale A del muro non e’ nota. La conduzione del calore attraverso il muro ha raggiunto un regime stazionario, di cui si conosce solo la temperatura delle interfacce : T1= 27 oC, T2= 22 oC , e T5 = -8 oC. Qual’e’ la temperatura dell’interfaccia T4?
Esercitazione n°6 di Fisica 1
Esercizio 1
Un blocco di argento di massa 280 g si trova alla temperatura di 20 oC, si vuole fondere il metallo, sapendo che la temperatura di fusione è 962 oC, che il calore specifico è cs = 236 J/Kg K e che il calore latente di fusione è LF= 105 KJ/Kg :
qual’è la quantità minima di calore, necessaria per fondere completamente il metallo?
Esercizio 2
Un foro circolare in un piatto d’alluminio ha diametro di 4,72 cm alla temperatura di 15 oC. Se si riscalda il piatto sino a 425 oC, calcolare: a) il diametro del foro quando il piatto viene scaldato a tale temperatura, il coefficiente di dilatazione lineare dell’alluminio e’ λ= 23 ·10-6 K-1 ;b) il diametro del foro nel caso in cui il piatto fosse di acciaio, il cui coefficiente di dilatazione lineare è λ= 11 ·10-6 K-1.
Esercizio 3
Una mole di ossigeno si espande a temperatura costante T di 280 K da un volume iniziale Vi di 11 L a un volume finale Vf di 18 L. Quanto lavoro svolge il gas in espansione?
Esercizio 4
Una macchina termica di Carnot opera tra due sorgenti di temperatura T1= 830 K e T2= 280 K . Ad ogni ciclo, che richiede 0, 23 s di tempo per essere completato, eroga 1200 J di lavoro. a)Qual’e’ il rendimento del motore? b) Qual’e’ la potenza media del motore? c) Quanto vale il calore |Q1| fornita dalla sorgente calda durante un ciclo? d) Quanto vale il calore |Q2| ceduto alla sorgente fredda durante un ciclo? e) Quanto vale la variazione di entropia del fluido legata all’assorbimento di calore dalla sorgente calda? f) Qual’e’ la variazione di entropia durante la cessione di calore alla sorgente fredda?
Esercitazione n°7 di Fisica 1
Esercizio 1
Una mole di gas idrogeno e’ scaldata a pressione costante da 300K a 420 K. Calcolare a) l’energia trasferita al gas tramite il calore, b) l’incremento di energia interna c) il lavoro svolto sul gas.
Esercizio 2
Si desidera che il soffitto di un’abitazione situata in una zona fredda abbia una resistenza termica R di 31,5 m2K/W. Per poter ottenere un tale isolamento termico che spessore dovrebbe avere una lastra di poliuretano espanso che ha una conducibilità termica pari a k= 0,024 W/(m K)? E di alluminio la cui conducibilità termica è k= 235 W/(m K)?
Esercizio 3
In un ciclo di
Carnot si ha un rendimento del 22,0 %. Le sue due sorgenti a temperatura
costante differiscono di 87,8 oC. Trovare a) la
temperatura maggiore e b) la temperatura minore.
Esercizio 4
Un condizionatore
d’aria opera tra le temperature di 21 oC e
34 oC e può prelevare dalla sorgente
fredda una potenza termica di 4,4 kW. La sua efficienza è il 29 % di quella di
un frigorifero di Carnot che operi tra le stesse temperature.
Qual’è l’efficienza del condizionatore d’aria? Che potenza
meccanica è richiesta dal motore elettrico del condizionatore?