ESERCITAZIONE n°1 (11/03/2014)

1 - Durante la scarica a terra di un fulmine scorre una corrente di 2,5·10⁴ A per un tempo di 20 μs. Quanta carica (a) viene trasferita da questo evento? Supponendo che tutta la carica venga trasferita da elettroni, quale è il numero degli elettroni (b) che si spostano tra la nuvola e il suolo?

2 - Quale deve essere la distanza tra una carica puntiforme q₁ = 26.0 μC e una carica puntiforme q₂ = 47 μC affinché la forza elettrica attrattiva tra di esse sial pari a 5,70 N?

3 - Le cariche e le coordinate di due particelle nel piano xy sono q₁ = + 3,0 μC, x₁ = 3,5 cm, y₁ = 0,50 cm, e q₂ = -4 μC, x₂ = -2,0 cm, y₂ = 1,5 cm. Si calcoli (a) l'intensità e (b) la direzione della forza elettrostatica agente su q₂. A che coordinate (c) x e (d) y dovrebbe essere posta una terza carica q₃ = +4 μC affinchè la forza elettrostatica netta agente su q₃ sia nulla?

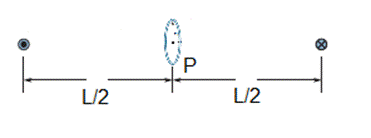
4 - Due particelle hanno carica q₁ = +3,20 10^-19 C e q₂ = +3,20 10^-19 C e occupano le posizioni x₁ = -3,00 m e x₂ = 3,00 m. Determinare il modulo (a) la direzione e il verso (b) del vettore campo elettrico presente nel punto P di coordinate x_P = 0,00 m e y_P = 4,00 m.

5 - A quale distanza, lungo l'asse di un disco di plastica carico di raggio R = 0,600 m, l'intensità del campo elettrico è uguale alla metà del campo che si ha al centro della superficie del disco?

6 - Si possono generare fasci di protoni ad alta velocità con appositi "cannoni" che accelerano i protoni per mezzo di campi elettrici. A quale accelerazione (a) è sottoposto un protone in un campo elettrico d'intensità pari a 2,00 10⁴ N/C? Che velocità (b) raggiunge il protone se viene accelerato da fermo per una distanza di 1,00 cm?

7 - Un dipolo elettrico costituito da cariche di intensità 1,50 nC e separate dalla distanza di 6,20 μm viene immerso in un campo elettrico d'intesità pari a 1100 N/C. Quale è il modulo del momento di dipolo (a)? Quale è la differenza tra le energie potenziali corrispondenti a orientamenti del dipolo concorde e discorde al campo (b)?

ESERCITAZIONE n°2 (18/03/2014)

1 – Si calcoli Φ_E attraverso (a) la base piatta e (b) la superficie curva di un emisfero di raggio R. Il campo E sia uniforme e parallelo all'asse dell'emisfero e le linee di E entrino attraverso la base piatta (si faccia uso della normale uscente).

2 – Sperimentalmente si trova che il campo elettrico in una certa regione dell'atmosfera della Terra è diretto verticalmente verso il basso. Ad una altitudine di 300 m il campo vale 50 N/C ed ad una altitudine di 200 m vale 110 N/C. Si trovi la quantità netta di carica contenuta in un cubo avente lato di 100 m e posizionato ad una altitudine tra i 200 e i 300 m. Si trascuri la curvatura della Terra.

3 – Su un conduttore isolato di forma arbitraria è presente una carica netta di +10·10^-6 C. All'interno del conduttore vi è una cavità nella quale è racchiusa una carica q = +3,0·10^-6 C. Quale è la carica (a) sulla parete della cavità e (b) sulla superficie esterna del conduttore? Si calcoli (c) il flusso elettrico totale uscente dalla superficie del conduttore.

4 – Una distribuzione rettilinea di carica infinita genera un campo di 4,5·10⁴ N/C a una distanza di 2,0 m. Si calcoli l'intensità di carica lineare.

5 – Si considerino due sottili e ampie lastre metalliche parallele e affaciate a breve distanza l'una dall'altra. Sulle loro facce interne è presente una carica di segno opposto con densità di modulo 7,00·10^-22 C/m². Si determini E, esprimendolo in notazione vettoriale, nei punti (a) esterni a entrambe le facce e (b) tra di esse.

6 – Due sfere concentriche cariche hanno raggi di 10,0 cm e 15,0 cm. La carica sulla sfera interna è 4,00·10^-8 C e quella sulla sfera esterna è 2,00·10^-8 C. Trovare il campo elettrico alla distanza (a) r 0 12,0 cm e (b) r = 20,0 cm.

ESERCITAZIONE n°3 (25/03/2014)

1 – Una batteria per auto da 12 V può far fluire una carica totale di 84 Ah attraverso un circuito, da un polo all'altro. (a) Quanti coulomb di carica ciò rappresenta? (b) Se tutta questa carica è sottoposta a una differenza di potenziale di 12 V, quanta energia viene utilizzata?

2 – Nella figura sottostante, qual è il potenziale netto nel punto P dovuto alle quattro cariche puntiformi, se V = 0 all'infinito , q = 5 fC e d = 4 cm?

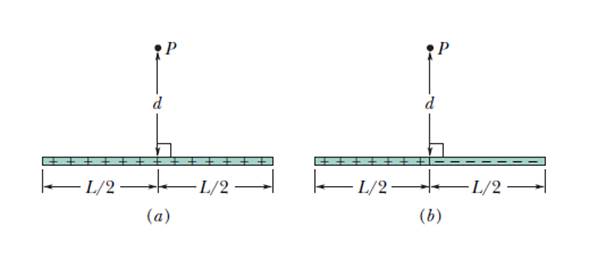
3 – (a) La figura a sottostante mostra una bacchetta isolante di lunghezza l = 6 cm e densità di carica lineare uniforme λ = +3,68 pC/m. Ponendo V = 0 all'infinito, si trovi il potenziale elettrico nel punto P a distanza d = 8 cm dal punto mediano della bacchetta. (b) La figura b mostra una bacchetta identica, ma divisa in due parti uguali. La parte destra ha carica negativa, le due parti hanno lo stesso modulo λ = 3,68 pC/m di densità di carica lineare uniforme. Si calcoli il potenziale elettrico nel medesimo punto P.

4 – Una sfera metallica avente raggio di 15 cm ha una carica netta di 3·10^-8 C. (a) Si trovi il campo elettrico sulla superficie della sfera. (b) Se V = 0 all'infinito qual è il potenziale elettrico sulla superficie della sfera? (c) A quale distanza dalla superficie della sfera il potenziale elettrico diminuisce di 500V?

ESERCITAZIONE n°4 (01/04/2014)

1 - Un condesatore piano ha piatti circolari aventi raggio di 8,20 cm distanti 1,30 mm l'uno dall'altro. (a) Si calcoli la capacità. (b) Quale carica comparirà sui piatti se si applica una differenza di potenziale di 120V?

2 - Nella figura sottostante si trovi (a) la capacità equivalente dell'insieme dei condensatori. Si assuma C₁ = 10,0 μF, C₂ = 5,0 μF e C₁ = 4,0 μF. Si trovino (b) la carica, (c) la differenza di potenziale e (d) l'energia immagazzinata nel condensatore 1 se V = 100 V.

3 - Un condensatore a piatti paralleli di area A = 0,034 m² e distanza d = 2,0 mm contiene un dielettrico di costante relativa pari a 5,5. Esso "si brucia" (cioè va in corto circuito incenerendo il dielettrico) quando l'intensità di campo tra i piatti eccede i 200 kN/C. Quanta energia vi si può immagazzinare al massimo?

4 - I fusibili nei circuiti elettrici sono costituiti da un filo metallico progettato in moda da fondere, e quindi interrompere il circuito, se la corrente che lo attraversa supera un determinato valore. Supponete che il materiale usato per un fusibile fonda quando la densità di corrente raggiunge i 440 A/cm². Che diametro deve avere il filo di forma cilindrica per ottenere un fusibile che limiti la corrente a 0,50 A?

5 – Quando si applica una tensione di 115 V su un filo di lunghezza pari a 10 m e di diametro pari a 0,30 mm, la densità di corrente è di 1,4·10⁴ A/m². Si trovi la resistività del filo.

6 – Una stufa elettrica alimentata da una tensione di 220 V ha una resistenza a incandescenza di 14,0 Ω a caldo. (a) Quanta potenza elettrica viene dissipata in calore? (b) Al prezzo di mercato di 0,10 euro/kWh, quanto costerà far funzionare la stufa per 5,0 h?

ESERCITAZIONE n°5 (08/04/2014)

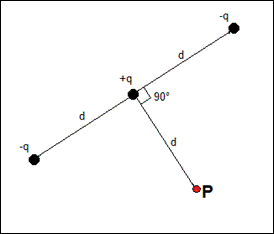
1 – Data la distribuzione discreta di cariche puntiformi raffigurata in figura, se il modulo delle cariche è q = 5 nC e d = 10 cm:

a) Calcolare il modulo del campo elettrico nel punto P.

b) Calcolare l'accelerazione iniziale di un protone (m = 1,672·10^-12 kg e e = 1,602·10^-19 C) lasciato libero di muoversi ed inizialmente fermo nel punto P.

2 – Si consideri una distribuzione lineare rettilinea di carica infinita:

a) Scrivere una espressione per il flusso totale elettrico uscente da una superficie cilinrica coassiale alla distribuzione di carica, avente raggio di base r = 1 m e altezza h = 5 m.

b) Si determini il modulo del campo elettrico a una distanza di 1 m se la densità di carica lineare ha modulo 3 μC/m.

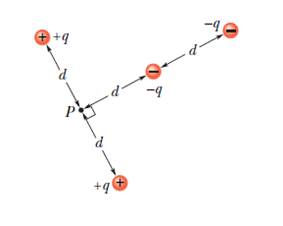
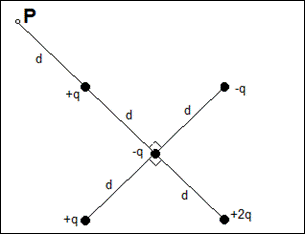
3 – Trovare il potenziale nel punto P dovuto alle cinque cariche puntiformi nella figura sottostante, se V = 0 all'infinito, q = 12 pC e d = 7 cm.

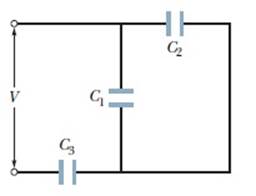
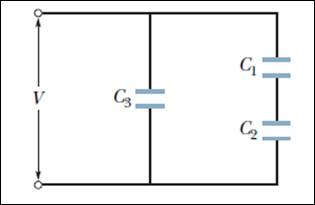
4 – Ai capi del circuito raffigurato nella figura sottostante è applicata una tensione V = 120 V. Siano i valori delle capacità C₁ = 5 pF, C₂ = 7 pF e C₃ = 4 pF:

a) Calcolare la capacità equivalente dell'insieme dei condensatori.

b) se ognuno dei condensatori viene interamente riempito con del polistirolo (ε_r = 2.6), quale sarà la capacità equivalente?

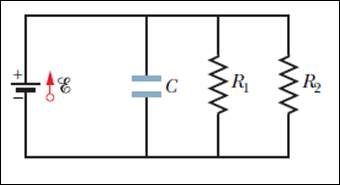
5 – Si consideri il circuito riportato in figura, in condizioni stazionarie. Siano R₁ = R₂ = 50 kΩ, C = 12 μF e V = 220 V.

a) Determinare il modulo della corrente che circola nel circuito.

b) Calcolare la potenza totale dissipata.

c) Calcolare l'energia immagazzinata nel condensatore C.

ESERCITAZIONE n°6 (15/04/2014)

1 – Un elettrone che ha velocità v = (2,0·10⁶ m/s)i + (3,0·10⁶ m/s)j attraversa un campo magnetico B = (0,03 T)i – (0,15 T)j:

a) Si calcoli il modulo e la direzione della forza che agisce sull'elettrone.

b) Si ripeta il calcolo per un protone avente la stessa velocità.

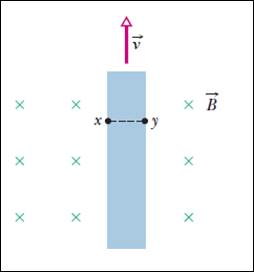
2 – Una striscia di metallo lungha 6,50 cm, larga 0,850 cm e spessa 0,760 mm si muove con velocità costante v attraverso un campo magnetico di intesità B = 1,20 mT perpendicolare alla striscia stessa come mostrato in figura. Fra i punti x e y compare una differenza di potenziale di 3,90 µV. Si determini la velocità v.

3 – Un elettrone avente energia cinetica di 1,20 keV si muove su un'orbita cicrcolare in un piano perpendicolare ad un campo magnetico uniforme. L'orbita ha raggio 25,0 cm. Si calcoli:

a) La velocità dell'eletrrone.

b) Il campo magnetico.

c) La frequenza di rivoluzione.

d) Il periodo di rivoluzione.

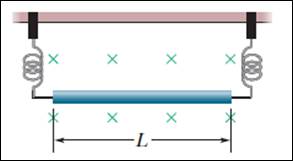
4 – Un cavo di lunghezza pari a 62,0 cm e di massa pari a 13,0 g è sospeso su di un paio di elettrodi elastici in un campo magnetico di 0,440 T (vedi figura). Si determini l'intesità(a) e il verso (b) della corrente nel cavo richiesta per annullare la tensione meccanica sugli elettrodi determinata dal peso del cavo.

ESERCITAZIONE n°7 (20/05/2014)

1 – Un lungo filo giace lungo l'asse x e porta una corrente di 30 A nella direzione positiva dell'asse x. Un secondo lungo filo è perpendicolare al piano xy, passa attraverso il punto (0; 4.0 m; 0), e trasporta una corrente di 40 A nella direzione positiva dell'asse z. Quale è l'intesità del campo magnetico risultante nel punto (0; 2.0 m, 0)?

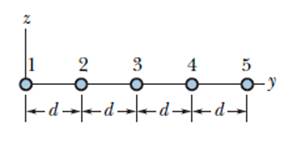
2 – In Figura, cinque lunghi fili paralleli giacienti nel piano xy sono separati da una distanza d = 50.0cm. Le correnti entranti nel piano della figura sono i1 = 2.00 A, i3 = 0.250 A, i4 = 4.00 A e i5 = 2.00 A; la corrente uscente dal piano è i2 = 4.00 A. Quale è l'intensità della forza netta per unità di lunghezza agente sul filo 3 dovuta alle correnti negli altri fili?

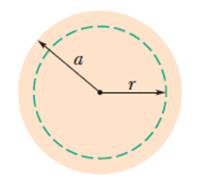
3 – La Figura mostra la sezione trasversale lungo il diametro di un conduttore cilindrico di raggio a = 2.00 cm trasportante una corrente uniforme di 170 a. Quale è l'intesità del campo magnetico alla distanza radiale (a) 0, (b) 1.00 cm, (c) 2.00 cm (superficie del filo) e (d) 4.00 cm?

4 – Un anello circolare di raggio 12 cm trasporta una corrente di 15 A. Una spira piatta di raggio 0.82 cm, avente 50 avvolgimenti e una corrente di 1.3 A, è concentrica all'anello. Il piano dell'anello è perpendicolare al piano della bobina. Supporre che il campo magnetico dell'anello sia uniforme attraverso la bobina. Quale è l'intensità (a) del campo magnetico prodotto dall'anello al suo centro e (b) del momento torcente sulla bobina dovuto all'anello?

ESERCITAZIONE n°8 (27/05/2014)

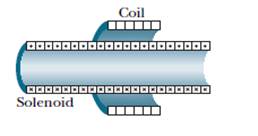
1 – In Figura una bobina di 120 avvolgimenti, di raggio 1,8 cm e resistenza 5,3 Ω è coassiale ad un solenoide di 220 avvolgimenti/cm e diametro 3,2 cm. La corrente nel solenoide passa da 1,5 A fino a zero in un intervallo Δt = 25 ms. Qual è la corrente indotta nel solenoide durante Δt?

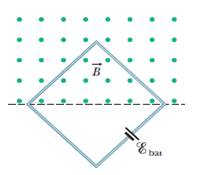
2 – Un circuito quadrato formato da un filo avente lato 2,00 m è perpendicolare ad un campo magnetico uniforme, con metà dell'area dell'anello immersa nel campo, come mostrato in Figura. Il circuito contiene una batteria ideale con fem E = 20,0 V. Se l'intensità del campo varia come B = 0,0420 – 0,870t, con B in tesla e t in secondi, quali sono: (a) la fem netta nel circuito e (b) la direzione della corrente (netta) attorno all'anello?

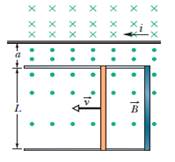
3 – La Figura mostra mostra una bacchetta di lunghezza L = 10,0 cm che viene forzata a muoversi con velocità costante v = 5,00 m/s lungo dei binari orizzontali. La bacchetta, i binari e la striscia di connessione sulla destra formano un circuito conduttore. La bacchetta ha resistenza 0,400 Ω, il resto del circuito ha una resistenza trascurabile. Una corrente i = 400 A che percorre il lungo filo ad una distanza a = 10,0 mm dal circuito determina un campo magnetico (non uniforme) attraverso l'anello. Trovare la fem (a) e la corrente (b) indotte nell'anello. Con quale rate (c) viene generata energia termica nella bacchetta? (d) Quale è l'intensità della forza che si deve applicare alla bacchetta per farla muovere di velocità costante? (e) A quale rate questa forza esercita lavoro sulla bacchetta?

4 – Una bobina circolare ha raggio di 10,0 cm e consiste di 30 stretti avvolgimenti del filo. Un campo magnetico esterno di intensità 2,60 mT è perpendicolare alla bobina. (a) Se non c'è corrente nella bobina, quale flusso magnetico connette le sue spire? (b) Quando la corrente nella spira è di 3,80 A in una certa direzione, si trova che il flusso netto attraverso la bobina svanisce. Quale è l'induttanza della bobina?

ESERCITAZIONE n°9 (29/05/2014)

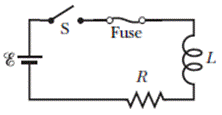
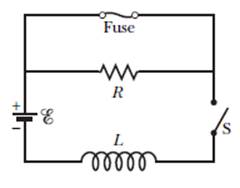
1 – In Figura, R = 15 Ω, L = 5,0 H, la batteria ideale ha E = 10 V, e il fusibile nel ramo superiore è un fusibile ideale da 3,0 A. Ha resistenza pari a zero finchè la corrente in esso rimane inferiore a 3,0 A. Se la corrente raggiunge i 3,0 A, il fusibile "salta" e successivamente ha resistenza infinita. L'interruttore S è chiso al tempo t = 0. (a) Quando salta il fusibile? (b) Disegnare un grafico della corrente i attraverso l'induttore in funzione del tempo, segnando l'istante nel quale il fusibile salta.

2 – Un magnete avente la forma di una bacchetta cilindrica ha una lunghezza di 5,00 cm e un diametro di 1,00 cm. Ha una magnetizzazione uniforme di 5,30·10³ A/m. Quale è il momento di dipolo magnetico?

3 – Il campo magnetico indotto alla distanza radiale di 6,0 mm dall'asse centrale di un capacitore circolare a piatti piani è 2,0·10^-7 T. Il raggio dei piatti è 3,0 mm. A quale rate dE/dt varia il campo elettrico tra i piatti?

4 – Un'onda elettromagnetica piana che viaggia nella direzione positiva dell'asse x nel vuoto ha componenti E_x = E_y = 0 e E_z = (2,0 V/m)cos[(π·10¹⁵ s^-1)(t – x/c)] (a) Qual è l'ampiezza della componente del campo magnetico? (b) Parallelamente a quale asse oscilla il campo magnetico? (c) Quando la componente del campo è nella direzione positiva dell'asse z in un certo punto P, quale è la componente del campo magnetico in quel punto?

ESERCITAZIONE n°10 (03/06/2014)

1 – Un elettrone avente velocità v = (0; 3·10⁶ m/s; 0) attraversa un campo magnetico costante B = (0,5 T; 0; 0).

a) Si determini la forza che agisce sulla particella (notazione vettoriale).

b) Si calcoli il raggio dell'orbita circolare che percorre la particella.

2 – Due fili paralleli di lunghezza infinita si trovano alla distanza di 50,0 cm, e sono percorsi dalle correnti i₁ = 2,0 A e i₂ = 2,0 A, aventi verso come indicato in Figura. Nel punto P, a metà della distanza tra i due fili, si trova il centro di una bobina circolare di raggio 5 cm, avente 10 avvolgimenti e percorsa da una corrente pari a 1 A, e che è perpendicolare alla congiungente tra i due fili.

a) Calcolare la forza agente tra i due fili e dire se è attrattiva o repulsiva.

b) Calcolare il modulo del campo elettrico nel punto P.

c) Calcolare il momento torcente τ sulla bobina dovuto ai due fili.

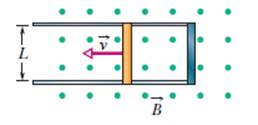
3 – In Figura si mostra una sbarretta di materiale conduttore, avente lunghezza 12 cm e resitenza di 9 Ω, che si muove con velocità costante v = 15 m/s lungo dei binari orizzontali, collegati tra loro e alla barretta a formare un circuito conduttore di resistenza trascurabile. Il sistema è immerso in un campo magnetico costante e uniforme uscente dal piano del circuito di intensità B = 0,25 T.

a) Trovare la f. e. m. indotta nel circuito.

b) Determinare l'energia dissipata nel circuito.

Quando la sbarretta arriva a fine corsa dei binari, aventi lunghezza di 30 cm, viene fermata.

c) Determinare l'induttanza del circuito nella sua configurazione finale.

4 – Si consideri il circuito in Figura. Si ha R = 20 Ω, L = 4 H, E = 12 V e il fusibile sia un fusibile ideale da 5 A. All'istante t = 0 il crcuito viene chiuso per mezzo dell'interruttore s.

a) Si calcoli dopo quando tempo il fusibile "salta".

b) Di determini l'energia magnetica totale immagazzinata nell'induttanza.