ESERCITAZIONE n°1 (08/10/2016)

1) Un podista parte da fermo e accelera di 1,5 m/s² per 3 s. Poi prosegue a velocità costante per altri 6 secondi. Calcolare la distanza totale percorsa.

2) Uno sciatore parte da fermo e accelera di 2 m/s² per 20 s. Poi prosegue a velocità costante per 30 secondi e infine decelera sino a fermarsi dopo altri 30 secondi. Calcolare:

a) la distanza percorsa

b) la velocità media

c) il tempo necessario per percorrere metà della distanza

3) Un auto della polizia è ferma a un posto di blocco. Uno scooter alla velocità costante di 60 km/h non si ferma all'alt. Dopo 3 s l'auto parte all'inseguimento, accelerando uniformemente sino a raggiungere la velocità di 90 km orari in 10 s. Calcolare:

a) l'accelerazione dell'auto della polizia;

b) il tempo necessario per raggiungere lo scooter;

c) la distanza percorsa dall'auto nell'istante in cui raggiunge lo scooter.

4) Una pietra è lanciata dalla cima di una scogliera con velocità iniziale verso l'alto pari a 20.0 m/s. La cima della scogliera si trova 50 m sopra il livello del mare. Determinare:

a) l'istante in cui la pietra raggiunge la massima altezza;

b) la massima altezza;

c) l'istante in cui la pietra ritorna alla quota dalla quale era stata lanciata;

d) la velocità della pietra in tale istante;

e) l'istante in cui la pietra raggiunge la superficie del mare.

5) Un ragazzo butta un sasso in un pozzo. Il suono dell'urto col fondo arriva 5 s dopo l'istante in cui lo ha lasciato cadere. Calcolare la profondità del pozzo. (Si consideri la velocità del suono pari a 340 km/h)

6) Due ciclisti procedono l'uno a fianco all'altro alla velocità di 30 km/h. Giunti a 200 metri dal traguardo, il primo accelera di 0.5 m/s2 per 8 s e poi prosegue a velocità costante sino al traguardo. Il secondo accelera di 0.3 m/s² sino al traguardo.

a) chi taglia per primo il traguardo?

b) Calcolare la distanza tra i due ciclisti nell'istante in cui il vincitore raggiunge la linea del traguardo.

ESERCITAZIONE n°2 (11/10/2016)

1) Una pietra è scagliata verso il cielo con velocità verticale iniziale pari a 40,0 m/s e velocità orizzontale iniziale pari a 8,00 m/s. Calcolare:

a) la velocità iniziale della pietra;

b) la velocità 5,00 s dopo il lancio;

c) il tempo necessario per raggiungere la massima altezza;

d) la massima altezza;

e) l'accelerazione orizzontale della pietra;

f) la gittata.

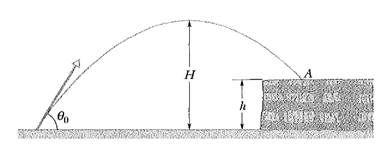
2) In figura è rappresentato un proiettile lanciato verso un terrapieno di altezza h con velocità iniziale di 42,0 m/s e angolo di lancio 60,0° sopra il piano orizzontale. Il proiettile cade nel punto A, 5,50 s dopo il lancio. Trovare:

a) l'altezza del terrapieno;

b) la velocità del proiettile all'impatto;

c) la massima altezza che esso ha raggiunto sopra il livello del terreno.

3) Un carosello di raggio 2,50 m è composta da due file di cavalli a dondolo. La fila più esterna si trova approssimativamente a una distanza dall'asse di rotazione pari al raggio del carosello. Quella più interna si trova a metà distanza tra la fila esterna e l'asse di rotazione. Il carosello si muove di moto circolare uniforme e compie una rotazione di 60,0° in 0,750 s. Calcolare:

a) la velocità angolare e tangenziale dei cavalli a dondolo della fila esterna;

b) la velocità angolare e tangenziale dei cavalli a dondolo della fila interna;

c) l'accelerazione centripeta dei cavalli a dondolo esterni ed interni;

d) l'accelerazione tangenziale dei cavalli a dondolo esterni ed interni;

e) il periodo del carosello;

f) la velocità media dei cavalli a dondolo esterni in un tempo pari al periodo.

4) Un auto viaggia alla velocità di 50,0 km/h. Un bambino al suo interno guarda la pioggia attraverso un finestrino lungo 1,00 m e alto 0,650 m. Egli nota una goccia di pioggia che percorre l'intera diagonale del finestrino. Calcolare:

a) la velocità della goccia nel sistema di riferimento del bambino;

b) la velocità della goccia nel sistema di riferimento di una persona ferma sul marciapiede.

N.B.1: Si supponga che all'esterno non ci sia vento e dunque la pioggia cada verticalmente.

N.B.2: Il moto di caduta delle gocce di pioggia è rettilineo uniforme (a = 0).

ESERCITAZIONE n°3 (18/10/2016)

1) Un blocco di massa 2,00 kg parte da fermo e, scivolando lungo un piano inclinato, arriva alla base dopo 4,00 s. A questo punto, il modulo della sua velocità è pari a 20,0 m/s. Calcolare:

a) l'angolo formato tra il piano inclinato e la base orizzontale;

b) la lunghezza del piano inclinato;

c) l'altezza e la base del piano inclinato;

d) la reazione vincolare che il piano esercita sul blocco.

2) Un blocco di 15,0 kg è posto su un piano orizzontale privo di attrito. Su di esso agiscono due forze: la prima ha modulo 10,0 N e forma un angolo di 30° col semiasse positivo delle ascisse; la seconda ha modulo 5,00 N e forma un angolo di 120° col medesimo semiasse. Calcolare:

a) l'accelerazione del blocco;

b) la reazione vincolare del piano;

c) la posizione del blocco dopo 10,0 s;

d) la velocità del blocco dopo 10,0 s.

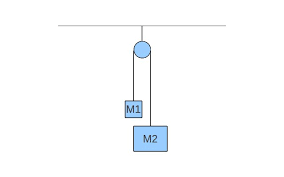
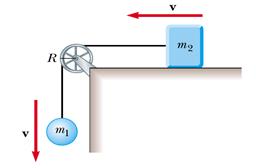
3) Due blocchi di massa 2,00 kg e 4,00 kg sono collegati tramite una fune e una carrucola di massa trascurabile. Calcolare:

a) l'accelerazione dei blocchi;

b) la tensione della fune;

c) la tensione del cavo d'acciaio che lega la carrucola al soffitto.

4) Alle estremità di una fune sono legati due blocchi di massa 300 g ciascuno. Praticato un foro su un tavolo privo di attrito, uno dei due blocchi è fatto calare all'interno del foro (senza che tocchi il suolo), l'altro è messo in rotazione sul piano orizzontale del tavolo. Nel sistema così realizzato il primo blocco è in equilibrio statico. Calcolare:

a) la tensione della fune;

b) la velocità del blocco che ruota.

5) Tre blocchi su un piano orizzontale liscio sono collegati tramite due funi. Sul primo blocco agisce una forza di 35,0 N . Poste m₁ = 5,00 kg , m₂ = 2,00 kg e m₃ = 3,00 kg , si calcoli

a) l'accelerazione di ciascun blocco;

b) la tensione delle due funi.

Esercitazione n° 4 (25/10/2016)

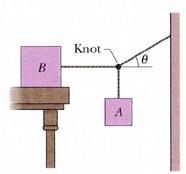
1) Il blocco B in figura pesa 711 N e il coefficiente di attrito statico tra esso e il piano di appoggio è pari a 0,250. L'angolo tra la fune e il piano orizzontale è di 30°. Trovare la massima massa del blocco A per cui il sistema è in equilibrio.

2) Un blocco di massa 3,00 kg parte da fermo e, sospinto da una forza orizzontale e costante di 100 N, si sposta dalla base alla cima di un piano inclinato in 10,0 s. Il piano inclinato forma un angolo di 30° rispetto alla base orizzontale e il coefficiente di attrito dinamico con il blocco è pari a 0,200. Calcolare:

a) la lunghezza del piano inclinato;

b) la velocità finale;

c) il lavoro della forza di attrito.

3) Due blocchi sono posti uno sopra l'altro su un piano orizzontale. Il blocco che sta sotto ha massa pari a 10,0 kg e il suo coefficiente di attrito col piano sottostante è pari a 0,150. Il blocco che sta sopra ha massa pari a 5,00 kg e il suo coefficiente di attrito col blocco sottostante è pari a 0,300. Improvvisamente viene applicata una forza esterna orizzontale sul blocco di 10,0 kg. Calcolare il massimo modulo di tale forza affinché il blocco di 5,00 kg rimanga attaccato al blocco sottostante.

4) Mediante una fune, si tira un blocco di 3.57 kg a velocità costante per una lunghezza di 4.06 m su un piano orizzontale. La forza applicata dalla fune sul blocco è di 7.68 N ed è diretta con angolo di 15° sopra al piano orizzontale. Determinare:

(a) il lavoro svolto dalla fune;

(b) l'aumento di energia termica del sistema blocco-piano;

(c) il coefficiente di attrito dinamico tra il piano e il blocco.

5) Si consideri un ascensore di massa 1800 kg e con un attrito pari a 4000 N.

a) Qual è la potenza sviluppata dal motore dell'ascensore quando quest'ultimo sale a una velocità costante di 3 m/s?

b) Quale sarebbe la potenza sviluppata dal motore se, a partire dalla velocità di 3 m/s, si volesse far accelerare l'ascensore di 1 m/s² verso l'alto?

Esercitazione n° 6 (08/11/2016)

1) Un ciclista parte da fermo al tempo t = 0 e accelera per 8.00 s. A questo punto la ruota (diametro: 66 cm) sta girando con una frequenza di 5.00 Hz. Nello stesso istante, il ciclista comincia a frenare fino a fermarsi all'istante t = 12 s.

a) Quanti giri ha fatto (in tutto) la ruota?

b) Che distanza ha percorso il ciclista?

c) Qual è stata la velocità lineare massima raggiunta?

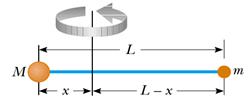
2) Dato il sistema in figura, calcolare il suo momento di inerzia supponendo M = 3.00 kg, m = 1.00 kg, L = 5.00 m, x = 1.50 m. Si supponga inoltre che la massa dell'asta che collega le due sfere sia di 2.00 kg.

3) Due blocchi di massa, rispettivamente, 2.00 kg e 6.00 kg sono connessi tramite un filo di massa trascurabile che passa attraverso una carrucola di raggio 0.250 m e massa 10.0 kg. La densità della carrucola è uniforme su tutto il disco. Il primo blocco si trova su un piano orizzontale mentre il secondo si trova su un piano inclinato di 45° rispetto alla base (vedi figura). Calcolare:

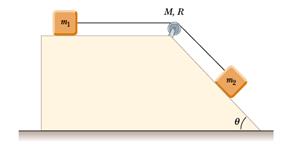a) l'accelerazione dei due blocchi;

b) la tensione alle due estremità del filo.

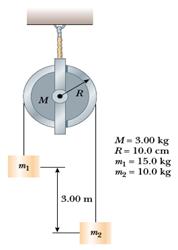4) Data la figura a lato, calcolare:

a) la velocità lineare dei due blocchi quando essi sono alla stessa altezza;

b) l'energia cinetica della carrucola.

(N.B. Considerare uniforme la densità di massa della carrucola)

5) Un'asta rigida di lunghezza 4 m e massa 3 kg è disposta verticalmente e può ruotare rispetto a un perno (“pivot”) posto alla sua estremità inferiore. L'asta parte da ferma e, sotto l'effetto della forza di gravità, ruota, passando per una configurazione orizzontale (vedi figura). In tale istante, calcolare:

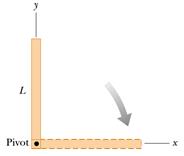a) la velocità angolare dell'asta;

b) la sua accelerazione angolare.

Esercitazione n° 7 (22/11/2016)

1) Un'asta uniforme del peso di 1200 N è sostenuta da un cavo (vedi figura). Nell'estremità inferiore dell'asta è presente un perno, mentre nell'estremità superiore è appeso un carico di 2000 N. Determinare:

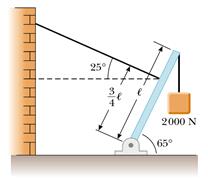
a) la tensione del cavo;

b) il modulo e la direzione della forza di reazione del pavimento sull'asta.

2) Una sfera di massa 2 kg e un blocco di massa 3 kg sono connessi per mezzo di una corda di massa trascurabile. La corda passa attraverso una carrucola di raggio 0.5 m e massa 1 kg. La massa della carrucola è concentrata nel cerchio esterno, mentre i raggi hanno massa trascurabile. Il blocco scivola senza attrito sulla superficie orizzontale. Determinare l'accelerazione lineare dei due oggetti utilizzando i concetti di momento angolare e di momento di una forza.

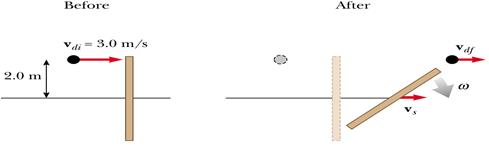
3) Un disco di massa 2 kg che si muove alla velocità di 3 m/s urta l'estremità di un'asta di massa 1kg, lunghezza 4 m e momento di inerzia 1.33 kg m², la quale giace su un piano ghiacciato di attrito trascurabile (vedi figura). Si assuma che la collisione sia elastica e che il disco non devi dalla direzione iniziale del suo moto. Determinare il modulo della velocità angolare dell'asta e delle velocità lineari del disco e dell'asta dopo l'urto.

4) Una ruota del vasaio (vedi figura) di raggio 0.5 m e massa 100 kg sta ruotando alla velocità di 50 giri/min. Per fermarla, il vasaio preme su di essa uno straccio bagnato, applicando una forza di 70 N per 6 s, in direzione radiale. Determinare il coefficiente di attrito dinamico tra la ruota e lo straccio

5) Una ruota di raggio 1 m, massa 5 kg e momento di inerzia 3 kg m² è montata su un asse orizzontale, come in figura. Una corda di massa trascurabile avvolta intorno alla ruota sostiene un oggetto di massa 20 kg. Determinare l'accelerazione angolare della ruota, l'accelerazione lineare dell'oggetto e la tensione della corda.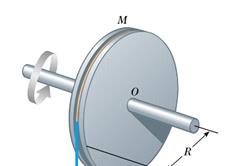

Esercitazione n° 8 (29/11/2016)

1) Posto m = 2 kg, k₁ = 7 N/m e k₂ = 11 N/m, calcolare il periodo di oscillazione dei seguenti sistemi usando l'approssimazione di piccole oscillazioni.

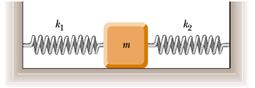
(a)

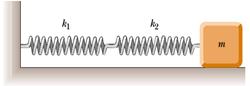
(b)

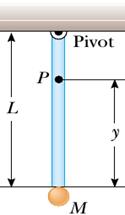
2) Si consideri il pendolo fisico in figura. Sia l'asta che la sfera hanno massa M = 7 kg. La lunghezza L dell'asta è pari a 10 m. Determinare:

a) la tensione nel punto P a quota y = 7.5 m;

b) il periodo di oscillazione del pendolo, nell'approssimazione di piccole oscillazioni

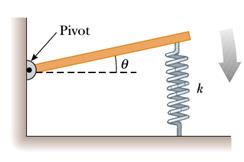
3) Posto L = 3 m e k = 5 N/m, calcolare la frequenza del sistema in figura, nell'approssimazione di piccole oscillazioni.

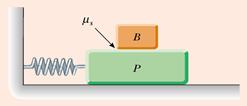
4) Due blocchi, P e B, sono connessi a un muro per mezzo di una molla e oscillano orizzontalmente (vedi figura). L'attrito col suolo è trascurabile. Sia f = 1.5 Hz la frequenza propria dell'oscillatore. Sperimentalmente, si osserva che la massima ampiezza di oscillazione che si può raggiungere mantenendo i due blocchi solidali tra loro (B non striscia su P) è 6.62 cm.

a) Determinare il coefficiente di attrito statico tra P e B.

b) Supposti m_P = 3 kg e m_B = 1 kg, determinare la costante elastica della molla.

Esercitazione n° 9 (06/12/2016)

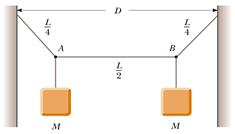
1) Un filo di massa 0.5 kg e lunghezza 5 m ha le sue estremità attaccate a due muri posti a distanza 3 m (vedi figura). Due oggetti, ciascuno di massa 2 kg, rimangono sospesi tramite il filo. Se un impulso d'onda viene generato nel punto A, determinare il tempo necessario affinché tale impulso raggiunga B.

2) Si consideri un pendolo semplice che oscilla su un piano verticale con un'ampiezza di oscillazione massima di 30°.

a) Calcolare il rapporto tra la frequenza di prima armonica del filo nell'istante in cui è inclinato di 30° e nell'istante in cui è disposto verticalmente.

b) L'approssimazione di piccole oscillazione non è valida per un angolo di 30°. Questo fatto cosa comporta? Il risultato al punto precedente può essere ritenuto valido?

c) Per pendolo semplice si intende che la massa del filo è trascurabile rispetto a quella della sfera appesa all'estremità inferiore dello stesso. Si supponga di sostituire il filo con una corda di massa comparabile a quella della sfera. Cosa cambia nella trattazione del problema? I risultati ottenuti al punto (a) sono ancora validi? Provare a ripetere i calcoli supponendo che la massa della corda sia identica a quella del peso posto all'estremità inferiore.

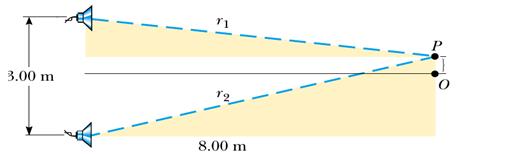
3) Due altoparlanti posti a 3 metri di distanza l'uno dall'altro emettono onde acustiche alla stessa frequenza e in fase. Un ascoltatore si trova inizialmente nel punto O, situato a 8 m dal centro della linea che connette i due altoparlanti (vedi figura). L'ascoltatore si sposta poi nel punto P (che si trova a una distanza di 0.35 m da O), trovando il primo minimo dell'intensità sonora. Qual è la frequenza delle onde sonore emesse degli altoparlanti?

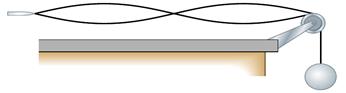
4) Un filo orizzontale è attaccato per un'estremità a una lama oscillante (si suppongano piccole oscillazioni, cosicché la punta della lama possa essere considerata un nodo). L'altra estremità è mantenuta in tensione per mezzo di una sfera di massa 2 kg. Il filo oscilla con una frequenza pari alla sua seconda armonica (vedi figura). Successivamente, la sfera viene rimpiazzata con una seconda sfera di massa differente. In seguito alla sostituzione, il filo ha una frequenza pari alla sua quinta armonica.

Determinare la massa della seconda sfera.

Esercitazione n° 10 (xx/xx/2016)