ESERCITAZIONE n°1 (13/10/2015)

1) Il conducente di un treno che viaggia alla velocità di 100 km/h nota che la stazione dista 500 m dalla posizione attuale del treno. Supponendo che egli voglia far arrestare il mezzo esattamente in corrispondenza della stazione e che i freni del treno generino una decelerazione costante pari a -3 m/s², quanti secondi deve attendere prima di iniziare a frenare?

2) Un auto sfreccia alla velocità costante di 162 km/h, superando un auto della polizia appostata su un lato della strada. Trascorso 1 s dall'istante del sorpasso, l'auto della polizia parte all'inseguimento della vettura, con un'accelerazione costante e pari a 3 m/s².

Dopo quanto tempo e a che distanza riuscirà a raggiungere l'autovettura?

3) Una pietra è lanciata dalla cima di una scogliera con velocità iniziale verso l'alto pari a 20.0 m/s. La cima della scogliera si trova 50 m sopra il livello del mare. Determinare:

a) l'istante in cui la pietra raggiunge la massima altezza;

b) la massima altezza;

c) l'istante in cui la pietra ritorna alla quota dalla quale era stata lanciata;

d) la velocità della pietra in tale istante;

e) l'istante in cui la pietra raggiunge la superficie del mare.

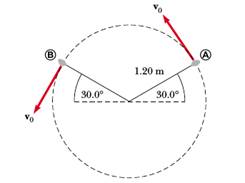
4) Una pietra attaccata all'estremità di una fionda viene fatta ruotare lungo una circonferenza verticale di raggio 1.2 m, alla velocità di 15.0 m/s (vedi figura). Il centro di rotazione si trova a un'altezza di 1.5 m rispetto al suolo.

a) Calcolare la gittata della pietra nel caso in cui essa abbandoni la fionda nel punto A e nel caso in cui abbandoni la fionda nel punto B.

b) Qual è l'accelerazione della pietra un istante prima di abbandonare la fionda nel punto A? E un istante dopo?

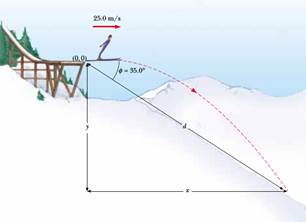
5) Un saltatore con gli sci abbandona la rampa con una velocità di modulo 25.0 m/s e diretta orizzontalmente (vedi figura). Il declivio sotto di lui ha un'inclinazione pari a 35° rispetto alla velocità iniziale dello sciatore. Determinare la distanza orizzontale (x) e verticale (y) percorse al momento in cui lo sciatore tocca il suolo.

ESERCITAZIONE n°2 (20/10/2015)

1) Un lampadario di massa 0.50 kg è sospeso tramite un cavo elettrico al soffitto del vagone di un treno. Supposto che il treno si muova di moto rettilineo con un'accelerazione costante pari a 3.00 m/s², si calcolino:

a) l'angolo che il cavo del lampadario forma con la verticale;

b) la tensione del cavo.

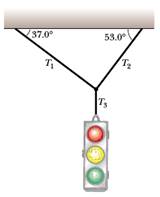
2) Un semaforo di massa 12.4 kg è appeso a un cavo legato ad altri due cavi, a loro volta attaccati ad un supporto rigido (vedi figura). I cavi superiori formano angoli di 37° e 53° rispetto al supporto orizzontale. Tali cavi possono reggere una tensione massima di 100 N, mentre il cavo verticale al quale è attaccato il semaforo può reggere una tensione massima di 200 N.

Determinare se i cavi in esame sono in grado di reggere il semaforo nella configurazione illustrata.

3) Una moneta è posta sopra un piano inclinato che forma un angolo θ rispetto all'asse orizzontale. Aumentando progressivamente l'angolo, si osserva che la moneta comincia a scivolare solo quando θ = 30°.

Calcolare il coefficiente di attrito statico tra la moneta e la superficie del piano.

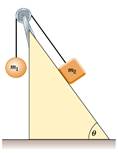
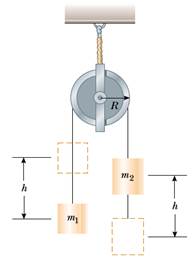
4) Due oggetti di massa m₁ = 2.0 kg e m₂ = 6.0 kg sono connessi da un filo di massa trascurabile che passa attraverso una carrucola (vedi figura). Supponendo θ = 55°, si determini, in assenza di attrito:

a) l'accelerazione dei due oggetti;

b) la tensione del filo;

c) la velocità di ciascun oggetto 2.0 s dopo che cominciano a muoversi.

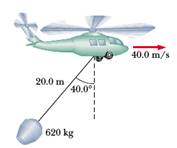
5) Un elicottero dei pompieri trasporta un grosso secchio del peso di 620 kg. Il secchio è legato a un cavo di lunghezza 20 m. Mentre l'elicottero vola alla velocità costante di 40 m/s, il cavo forma un angolo di 40° con la verticale. Il secchio ha una sezione trasversale pari a 3.8 m² rispetto al piano perpendicolare al vettore velocità dell'elicottero.

Determinare il coefficiente di resistenza aerodinamica, assumendo che la forza di attrito sia proporzionale al quadrato della velocità del secchio.

ESERCITAZIONE n°3 (27/10/2015)

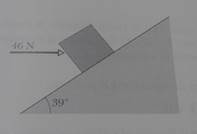
1) Un blocco di 4.8 kg su un piano inclinato di 39° rispetto all'orizzontale è spinto da una forza orizzontale di 46 N (vedi figura). Il coefficiente di attrito dinamico tra il blocco e il piano è di 0.33.

Supposto che la velocità iniziale del blocco abbia modulo 4.3 m/s e sia diretta parallelamente al piano inclinato e verso l'alto:

a) Quanto vale l'accelerazione del blocco?

b) Quanta strada percorre prima di fermarsi?

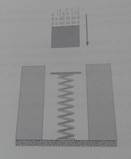
2) Un blocco di 263 g è lasciato cadere verticalmente su una molla di costante elastica k = 2.52 N/cm. Il blocco colpisce la molla che si accorcia di 11.8 cm prima di fermarsi momentaneamente. Trascurando gli attriti:

a) Quanto lavoro viene compiuto nella compressione della molla dalla forza di gravità? E dalla forza elastica?

b) Quanto vale la velocità del blocco un istante prima di colpire la molla?

c) Se la velocità iniziale del blocco raddoppia, di quanto viene compressa la molla?

3) Si consideri un ascensore di massa 1800 kg e con un attrito pari a 4000 N.

a) Qual è la potenza sviluppata dal motore dell'ascensore quando quest'ultimo sale a una velocità costante di 3 m/s?

b) Quale sarebbe la potenza sviluppata dal motore se, a partire dalla velocità di 3 m/s, si volesse far accelerare l'ascensore di 1 m/s² verso l'alto?

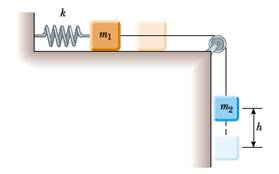
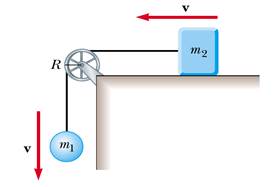
4) Due blocchi sono connessi da un filo sottile che passa attraverso una carrucola priva di attrito (vedi figura). Un blocco (di massa 2 kg) giace sul piano orizzontale ed è attaccato a una molla di costante elastica 20 N/m. Nell'istante in cui il sistema viene lasciato libero di muoversi, la molla si trova nella sua lunghezza di riposo. Se il secondo blocco (di massa 1 kg) scende di 50 cm prima di arrestarsi, calcolare il coefficiente di attrito dinamico tra il primo blocco e il piano orizzontale.

5) Mentre corre, un podista dissipa 0.6 J di energia meccanica ad ogni falcata e per ogni kg di massa corporea. Se un podista ha massa pari a 60 kg e dissipa una potenza di 70 W durante la corsa, a che velocità si sta muovendo? Si assuma che l'ampiezza della falcata sia pari a 1.5 m.

ESERCITAZIONE n°4 (03/11/2015)

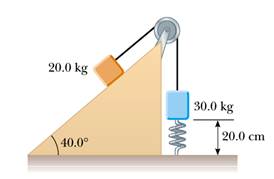
1) Due blocchi di 20 kg e 30 kg sono connessi per mezzo di un filo che passa attraverso una carrucola senza attrito e di massa trascurabile. Il blocco da 30 kg è connesso a una molla di massa trascurabile e con una costante di forza pari a 250 N/m. Nella configurazione mostrata in figura, la molla è alla sua lunghezza di equilibrio. Il piano è privo di attrito. Dopodiché, il blocco da 20 kg è tirato giù di 20 cm lungo il piano inclinato e, successivamente, lasciato libero di muoversi.

Determina la velocità di ciascun blocco quando il blocco di 30 kg si trova a 20 cm dal suolo.

2) Mediante una fune, si tira un blocco di 3.57 kg a velocità costante per una lunghezza di 4.06 m su un piano orizzontale. La forza applicata dalla fune sul blocco è di 7.68 N ed è diretta con angolo di 15° sopra al piano orizzontale. Determinare:

(a) il lavoro svolto dalla fune;

(b) l'aumento di energia termica del sistema blocco-piano;

(c) il coefficiente di attrito dinamico tra il piano e il blocco.

3) Un carrello, all'interno di una miniera, ha massa 950 kg e si muove in salita su delle rotaie che formano un angolo di 30° rispetto all'orizzontale. Il carrello parte da fermo, ed è accelerato per mezzo di un cavo collegato ad un argano a motore. L'accelerazione è costante e il carrello raggiunge la velocità di 2.2 m/s in 12 s. Dopodiché, continua a muoversi a velocità costante.

Trascurando l'attrito:

(a) Che potenza deve sviluppare l'argano quando il carrello si muove a velocità costante.

(b) Qual è la massima potenza sviluppata dall'argano?

(c) Qual è il lavoro totale compiuto dall'argano sul carrello alla fine del percorso (che ha una lunghezza complessiva di 1250 m)?

4) Un blocco di massa 3.18 kg parte da fermo e scivola senza attrito lungo un piano inclinato di 32° rispetto all'orizzontale. Alla fine del piano, è installata una molla con costante elastica pari a 11502 N/m (vedi figura). Il blocco si ferma momentaneamente dopo aver compresso la molla di 5.48 cm.

(a) Quanta strada ha percorso il blocco sino a quell'istante?

(b) Qual è la velocità del blocco un istante prima di toccare la molla?

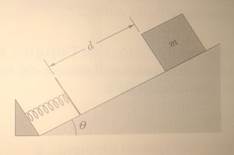
5) Il coefficiente di attrito dinamico tra il blocco di 3 kg e la superficie in figura è pari a 0.4. Il sistema parte da fermo. Qual è la velocità della sfera di 5 kg quando essa è scesa di 1.5 m?

ESERCITAZIONE n°5 (10/11/2015)

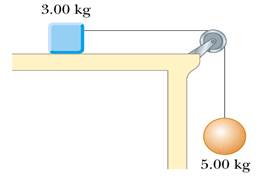
1) Una sfera di massa 0.2 kg si muove verso destra alla velocità di 150 m/s mentre una sfera di massa 0.3 kg si muove verso sinistra alla velocità di 0.4 m/s. Le due sfere si scontrano frontalmente con un urto perfettamente elastico. Determinare:

a) Le velocità delle due sfere dopo la collisione;

b) la velocità del centro di massa prima e dopo la collisione.

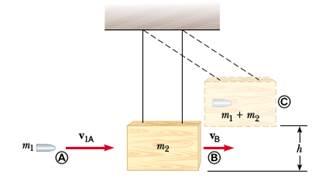
2) Un proiettile di massa 10 g è sparato contro un blocco di legno di massa 1.1 kg, connesso ad un sostegno rigido per mezzo di un filo inestensibile di massa trascurabile e lunghezza 1 m. Il proiettile rimane conficcato al interno del blocco, il quale oscilla di un angolo di 60° rispetto alla verticale. Determinare la velocità iniziale del proiettile.

3) Romeo (77 kg) e Giulietta (55 kg) sono a bordo di una barca a remi su un lago. Romeo siede a poppa, Giulietta a prua. La barca ha una massa di 80 kg (senza contare i passeggeri) e una lunghezza complessiva di 2.7 m. Qualora Giulietta voglia andare a sedersi affianco a Romeo, di quanto si muoverebbe la barca rispetto alle acque immobili del lago? E in quale direzione?

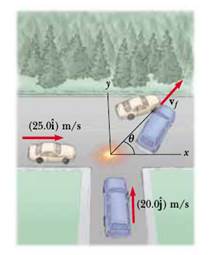
4) Una macchina di massa 1500 kg in viaggio verso est alla velocità di 25 m/s, si scontra con una seconda auto di massa 2500 kg in viaggio verso nord con velocità 20 m/s (vedi figura). Supponendo che dopo lo scontro le due auto rimangano attaccate (urto anelastico), determinare il modulo la direzione e il verso della velocità delle due auto dopo la collisione.

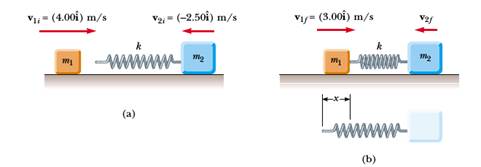
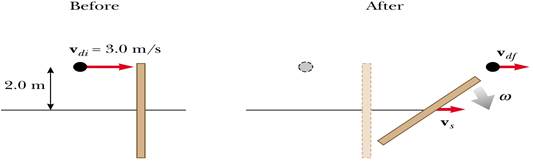
5) Un blocco di massa 1.6 kg, in moto verso destra alla velocità costante di 4 m/s su un piano orizzontale privo di attrito, urta una molla connessa con un secondo blocco di massa 2.1 kg, inizialmente in moto verso sinistra alla velocità costante di 2.5 m/s (vedi figura). La costante elastica della molla è pari a 600 N/m.

a) Determinare le velocità dei due blocchi dopo la collisione;

b) Determinare la velocità del secondo blocco, nel istante in cui la velocità del primo blocco è pari a 3 m/s (verso destra);

c) Determinare la compressione della molla nell'istante discusso nel punto b)

d) Determinare la massima compressione della molla durante l'urto

ESERCITAZIONE n° 6 (23/11/2015)

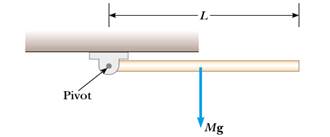
1) Un'asticella uniforme di lunghezza 50 cm e massa 1 kg è attaccata a un estremità ad un fulcro, attorno al quale è libera di ruotare sul piano verticale (vedi figura). L'asticella parte da ferma dalla posizione orizzontale. Si calcoli l'accelerazione angolare all'istante iniziale. Si determini inoltre l'accelerazione lineare dell'estremità destra della sbarretta.

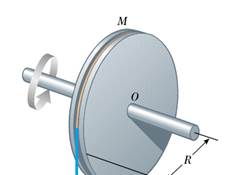
2) Una ruota del vasaio (vedi figura) di raggio 0.5 m e massa 100 kg sta ruotando alla velocità di 50 giri/min. Per fermarla, il vasaio preme su di essa uno straccio bagnato, applicando una forza di 70 N per 6 s, in direzione radiale. Determinare il coefficiente di attrito dinamico tra la ruota e lo straccio

3) Una ruota di raggio 1 m, massa 5 kg e momento di inerzia 3 kg m² è montata su un asse orizzontale, come in figura. Una corda di massa trascurabile avvolta intorno alla ruota sostiene un oggetto di massa 20 kg. Determinare l'accelerazione angolare della ruota, l'accelerazione lineare dell'oggetto e la tensione della corda.

4) Due cilindri di massa 4 kg e 2 kg sono connessi per mezzo di un filo passante per una carrucola di raggio 0,5 m e momento di inerzia 1 kg m² rispetto al suo asse di rotazione (vedi figura). Il sistema parte da fermo. Determinare le velocità lineari dei cilindri nell'istante in cui il cilindro più pesante è sceso di una distanza di 1,5 m. Si determini inoltre la velocità angolare della carrucola nel medesimo istante.

5) Una trottola di momento di inerzia 4 x 10^-4 kg m², parte da ferma ed è libera di ruotare lungo l'asse verticale. Il filo, inizialmente avvolto intorno alla trottola, viene tirato con una forza costante di 5.57 N. Determinare la velocità angolare finale della trottola qualora la lunghezza del filo sia pari a 80 cm.

ESERCITAZIONE n°7 (03/12/2015)

1) Una sfera di massa 2 kg e un blocco di massa 3 kg sono connessi per mezzo di una corda di massa trascurabile. La corda passa attraverso una carrucola di raggio 0.5 m e massa 1 kg. La massa della carrucola è concentrata nel cerchio esterno, mentre i raggi hanno massa trascurabile. Il blocco scivola senza attrito sulla superficie orizzontale. Determinare l'accelerazione lineare dei due oggetti utilizzando i concetti di momento angolare e di momento di una forza.

2) Un papà con la sua bambina giocano su un'altalena basculante (vedi figura). Il padre ha una massa di 70 kg, la bambina di 35 kg. L'altalena può essere considerata come un'asta rigida di massa 40 kg e lunghezza 3 m. Il fulcro è privo di attrito. Determinare:

a) il modulo del momento angolare quando l'altalena ha una velocità angolare pari a 2 rad/s;

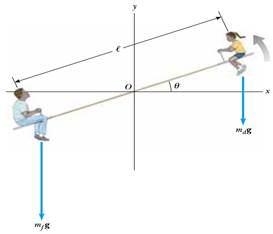b) il modulo dell'accelerazione angolare del sistema quando l'altalena forma un angolo di 30 gradi con il piano orizzontale (vedi figura).

3) Un disco di massa 2 kg che si muove alla velocità di 3 m/s urta l'estremità di un'asta di massa 1kg, lunghezza 4 m e momento di inerzia 1.33 kg m², la quale giace su un piano ghiacciato di attrito trascurabile (vedi figura). Si assuma che la collisione sia elastica e che il disco non devi dalla direzione iniziale del suo moto. Determinare il modulo della velocità angolare dell'asta e delle velocità lineari del disco e dell'asta dopo l'urto.

4) Una trave uniforme di lunghezza 8 m e peso 200 N è attaccata a un cavo, il quale a sua volta è at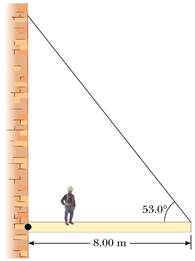taccato a un muro tramite un perno (vedi figura). La trave si trova in posizione orizzontale, mentre un uomo di peso 600 N sta in piedi su di essa a una distanza di 2 m dal muro. L'angolo tra la trave e il cavo che la sostiene è pari a 53°. Il sistema così descritto si trova in equilibrio. Determinare:

a) la tensione del cavo;

b) Il modulo e la direzione della forza esercitata dal muro sulla trave;

c) il valore minimo del coefficiente di attrito statico tra il muro e la trave.

ESERCITAZIONE n°8 (15/12/2015)

1) Un'onda sinusoidale viaggia nel verso negativo della direzione x di un sistema di riferimento cartesiano. L'onda ha ampiezza pari a 15 cm e frequenza di 8 Hz. La distanza spaziale tra due creste d'onda consecutive è pari a 40 cm. La posizione verticale y della perturbazione nel punto x = 0 all'istante t = 0 è pari a 7.5 cm. Determinare l'equazione d'onda y(x,t).

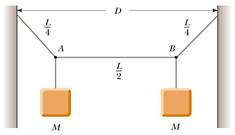
2) Un filo di massa 0.5 kg e lunghezza 5 m ha le sue estremità attaccate a due muri posti a distanza 3 m (vedi figura). Due oggetti, ciascuno di massa 2 kg, rimangono sospesi tramite il filo. Se un impulso d'onda viene generato nel punto A, determinare il tempo necessario affinché tale impulso raggiunga B.

3) Una corda tesa ha massa 0.180 kg e lunghezza 3.6 m. Quale potenza dev'essere fornita per generare delle onde sinusoidali che abbiano ampiezza 0.1 m, lunghezza d'onda 0.5 m e che viaggino alla velocità di 30 m/s?

4) Un'onda che viaggia su un filo teso è descritta dalla funzione

a) Quanta energia viene trasmessa nell'unità di tempo lungo il filo se la sua densità di massa lineare è pari a 75 g/m?

b) Qual è l'energia contenuta in ogni ciclo dell'onda?

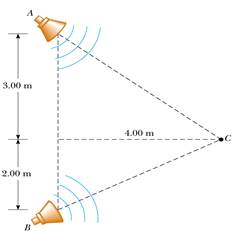
5) Due altoparlanti emettono onde acustiche a diversa frequenza. L'altoparlante A ha un output di 1.00 mW, l'altoparlante B ha un output di 1.50 mW. Determinare il volume percepito nel punto C (in decibel).

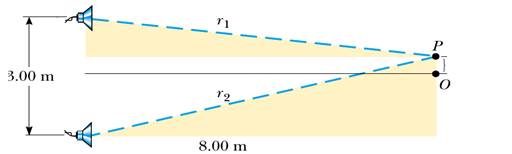
6) Due altoparlanti posti a 3 metri di distanza l'uno dall'altro emettono onde acustiche alla stessa frequenza e in fase. Un ascoltatore si trova inizialmente nel punto O, situato a 8 m dal centro della linea che connette i due altoparlanti (vedi figura). L'ascoltatore si sposta poi nel punto P (che si trova a una distanza di 0.35 m da O), trovando il primo minimo dell'intensità sonora. Qual è la frequenza delle onde sonore emesse degli altoparlanti?

ESERCITAZIONE n°9(08/01/2015)

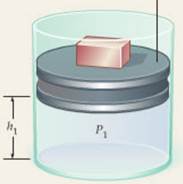
1) Un contenitore cilindrico di sezione pari a 1 m2 è dotato di uno stantuffo (vedi figura). All'interno del cilindro è contenuto un gas ideale. La pressione applicata dallo stantuffo sul gas è pari a 130 kPa; l'altezza della base dello stantuffo rispetto alla base del cilindro è pari a 25 cm. La temperatura del sistema è di 290 K.

a) Si supponga di aumentare la pressione sul gas sino a 170 kPa e si assuma che la temperatura non vari. Deteminare l'altezza finale dello stantuffo.

b) Si supponga invece di mantenere costante la pressione (130 kPa) e far variare la temperatura dal valore iniziale di 290 K al valore finale di 330 K. Determinare l'altezza finale dello stantuffo.

2) Determinare la massa di vapore alla temperatura iniziale di 130 °C necessaria per riscaldare 200 g di acqua contenuta in un bicchiere di vetro di 100 g, entrambi alla temperatura iniziale di 20 °C, alla temperatura finale di 50 °C.

(Calore specifico del vetro: 837 J/kg °C; Calore specifico del vapore: 2010 J/kg °C; Calore latente del vapore: 2260 kJ/kg)

3) Una mole di gas ideale è mantenuto alla temperatura costante di 0.0 °C durante un'espansione da 3.0 L a 10.0 L.

a) Determinare il lavoro svolto dal sistema durante l'espansione.

b) Determinare la quantità di calore scambiata con l'ambiente esterno durante l'espansione.

c) Supponendo di riportare il sistema al volume iniziale per mezzo di una trasformazione isobara, determinare il lavoro svolto sul sistema.

4) Una macchina termica con un efficienza del 24% svolge un lavoro di 1250 J. Determinare:

a) il calore assorbito dal termostato ad alta temperatura;

b) il calore ceduto al termostato a bassa temperatura

5)

a) Calcolare la variazione di entropia che si verifica con lo scioglimento di un cubetto di ghiaccio di 125 g alla temperatura di 0 °C. Si assuma che la fusione avvenga in maniera reversibile.

b) In seguito al completo scioglimento del cubetto, si supponga che l'acqua, alla temperatura di 0 °C, ceda calore in maniera reversibile a un termostato, causando una diminuzione dell'entropia di 112 J/K nel sistema formato dall'acqua stessa. Determinare la massa di acqua che si congela in tale processo.

ESERCITAZIONE n°10(11/01/2015)

Preparazione al II test in Itinere

1) Un pizzaiolo fa roteare una sfera di raggio 10 cm di impasto per pizza, sino a ridurla a un disco di spessore 5 mm. La frequenza di rotazione iniziale dell'impasto (quando è ancora sferico) è pari a 7 Hz. Si supponga che la densità dell'impasto sia costante in tutto il processo e che gli attriti siano trascurabili. Determinare:

a) l'accelerazione centripeta a cui è sottoposto un punto sul bordo del disco;

b) la frequenza di rotazione finale.

c) Supponendo che l' energia cinetica rotazionale dell'impasto sia pari a 0.193 J, determinarne la massa.

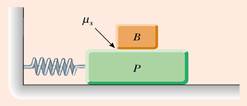
2) Due blocchi, P e B, sono connessi a un muro per mezzo di una molla e oscillano orizzontalmente (vedi figura). L'attrito col suolo è trascurabile. Sia f = 1.5 Hz la frequenza propria dell'oscillatore. Sperimentalmente, si osserva che la massima ampiezza di oscillazione che si può raggiungere mantenendo i due blocchi solidali tra loro (B non striscia su P) è 6.62 cm.

a) Determinare il coefficiente di attrito statico tra P e B.

b) Supposti m_P = 3 kg e m_B = 1 kg, determinare la costante elastica della molla.

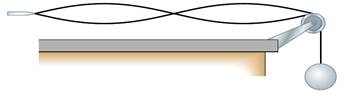
3) Un filo orizzontale è attaccato per un'estremità a una lama oscillante (si suppongano piccole oscillazioni, cosicché la punta della lama può essere considerata un nodo). L'altra estremità è mantenuta in tensione per mezzo di una sfera di massa 2 kg. Il filo oscilla con una frequenza pari alla sua seconda armonica (vedi figura). Successivamente, la sfera viene rimpiazzata con una seconda sfera di massa differente. In seguito alla sostituzione, il filo ha una frequenza pari alla sua quinta armonica.

Determinare la massa della seconda sfera.

4) Una macchina termica di Carnot ha efficienza del 26%. La sorgente fredda ha temperatura pari a 295 K.

a) Determinare la temperatura della sorgente calda.

b) Si supponga che, in un ciclo, il lavoro prodotto sia pari a 500 J. Determinare la variazione di entropia nella sorgente calda e, separatamente, la variazione di entropia nella sorgente fredda.