ESERCITAZIONE n°1 (08/10/2015)

1.      Si risolvano i seguenti eserciti di conversione:

( a ) 

 

( b )

 

( C )

 

2.      Un'auto aumenta uniformemente la sua velocità da 25 a 55km/h in 0.50min. Un ciclista accelera uniformemente da fermo a 30km/h in 0.50min. Calcolare le rispettive accelerazioni.

 

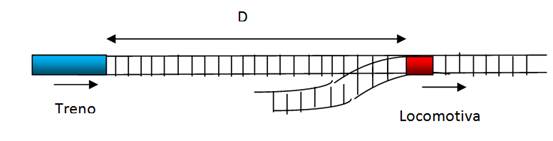
3.      All'uscita da una curva, il macchinista di un treno che sta viaggiando a 100km/h = 27.8m/s si accorge che una locomotiva è entrata erroneamente nel binario da una diramazione posta 0.42km più avanti, come in figura. La locomotiva viaggia a 18km/h. Il macchinista aziona immediatamente la frenatura rapida. (a) Quale deve essere il valore assoluto minimo dell'accelerazione costante impressa dal freno per evitare una collisione?

 
 

4.      Un'auto sale una collina alla velocità costante di 40km/h e ridiscende dalla stessa strada a 60km/h. Calcolare le velocità medie complessive (scalari e vettoriali) per andata e ritorno.

 

5.      In un cantiere una chiave inglese, lasciata cadere inavvertitamente, arriva al suolo alla velocità di 24 m/s. (a) Da che altezza è caduta? (b) quanto tempo ha impiegato per cadere?

 

 

ESERCITAZIONE n°2 (14/10/2015)

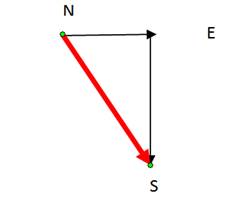
1.      Un aeroplano vola per 300 km verso est dalla città A alla città B in 45 min, e quindi per 600 km a sud da B a C in 1; 50 h. (a) Quale vettore spostamento corrisponde al viaggio completo? Quali sono (b) il vettore velocità media e (c) la velocità scalare media complessiva?

 

2.     

Q
 
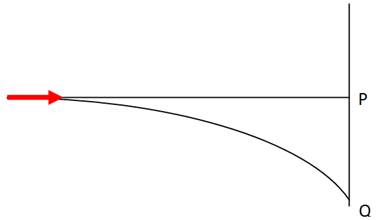
Una freccetta viene lanciata orizzontalmente in direzione del centro del bersaglio P in figura con velocità  v0 = 10 m/s. Dopo 0, 19 s essa colpisce il punto Q sul bordo del bersaglio posto verticalmente sotto P. Calcolare (a) la distanza PQ e la distanza dal bersaglio alla quale si trovava il lanciatore.

 

3.      Un proiettile viene sparato orizzontalmente da un'arma posta a 45,0 m sopra un terreno orizzontale. La sua velocità alla bocca dell'arma è 250 m/s. Calcolare il tempo di volo, a che distanza orizzontale raggiungerà il terreno e il modulo della componente verticale della velocità quando colpisce il terreno.

 

4.      La luna gira attorno alla Terra compiendo un giro completo in 27,3 giorni. Si assuma l’orbita circolare con raggio pari a 385000 Km.  (a) Qual è il modulo dell’accelerazione centripeta della Luna?

 

5.      La ventola di ventilatore ruota compiendo 1200 giri al minuto. Consideriamo un punto sul bordo esterno di una pala di raggio 0,15 m. (a) Che distanza percorre il punto ad ogni giro? (b) Qual è la sua velocità angolare e lineare? (c) La sua accelerazione? (d) Qual è il periodo di questo moto?

 

ESERCITAZIONE n°3 (22/10/2015)

1. Un'auto che viaggia a 53 km/h va a sbattere contro la spalletta di un ponte. Un passeggero seduto  all'interno si sposta in avanti, rispetto alla strada, di 65 cm fino  a che si arresta per l'intervento dell' airbag. Trovare l'intensità della forza, supposta costante, che agisce sul busto del passeggero, che ha una massa di 41 kg.

 

2. Una ragazza di 40 kg e una slitta di 8,4 kg sono sulla superficie di un lago gelato, distanti tra loro 15m. Per tirare a sé la slitta, la ragazza, per mezzo di una fune di massa trascurabile, esercita sulla slitta una forza orizzontale di 5,2N. (a) Qual è  l'accelerazione della slitta? (b) Qual è l'accelerazione della ragazza? (c)A quale distanza si incontreranno, in assenza di attrito, a partire dalla posizione iniziale della ragazza?

 

3. Una scimmia di 11 Kg si arrampica lungo una fune di massa trascurabile passata ( senza attrito) per il ramo di un albero. All’ altro capo e’ fissata una massa di 15 Kg.

(a)    Qual è la minima accelerazione con cui la scimmia deve arrampicarsi sulla fune in modo da sollevare la massa di 15 kg dal suolo?

(b)    Se, una volta sollevato il peso, la scimmia si ferma e rimane appesa alla fune, quale sarà ora la sua accelerazione?

(c)    E la tensione della fune?

 

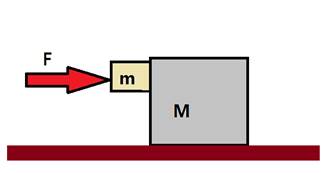
4. I due blocchi della figura rispettivamente di massa m = 16 Kg e M = 88Kg , non sono collegati tra loro. Il coefficiente di attrito tra i blocchi è µs = 0,38  , mentre la superficie su cui appoggia M è priva d’attrito. Qual è l’intensità minima della forza orizzontale F necessaria per mantenere m contro M senza che cada giù?

 

 

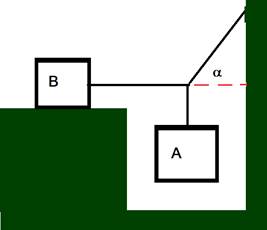
5. Il blocco B in figura pesa 711 N e il coefficiente d’attrito statico tra blocco e piano orizzontale di appoggio è  . Trovate il massimo peso del blocco A per cui il sistema è in equilibrio assumendo che la corda attaccata a B sia orizzontale (considerare l’angolo a= 41°).

 

 

 

 

ESERCITAZIONE n°4 (29/10/2015)

 

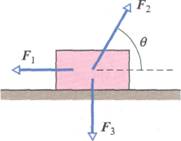
1.      La figura in basso mostra tre forze applicate ad una cassa che scivola verso sinistra di 3,00 metri su un piano lubrificato. I loro moduli sono  ,  ,  e l’angolo θ vale 60,0°. Durante lo spostamento (a) quanto vale il lavoro totale svolto sulla cassa dalle tre forze?

(b) L’ energia cinetica della cassa cresce o diminuisce?

 

 

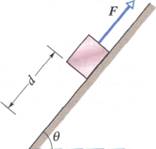
2.      Il blocco di ghiaccio della figura scivola senza attrito giù per una rampa inclinata di  θ = 50°, trattenuto da una corda cui è applicata una forza F di modulo 50 N. Il blocco guadagna 80 J di energia cinetica in un tratto d = 0,50 m. Quanto maggiore sarebbe il guadagno se il blocco precipitasse liberamente?

3.      Tarzan, la cui massa è di 81,63 Kg, salta da una roccia appeso a una prov­videnziale liana lunga 15,24 m (vedi la figura). Dall'alto della roc­cia al punto più basso della sua oscillazione Tarzan scende  di 3,2 m. La liana è soggetta a rompersi se la tensione su di essa supera 1100 N.  Riesce a resistere al salto senza spezzarsi?

 

 

 

 

 

 

 

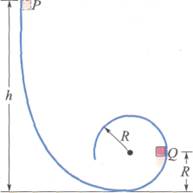
4.      Un blocchetto di massa m scivola senza attrito lungo una guida ripiegata ad anello come in figura.

               Se parte da fermo in P, trovare la forza risultante che agisce su di esso nel punto Q (supporre h =           5R). Trovare poi da quale altezza rispetto al fondo dell'anello deve scendere il blocchetto perché la forza     esercitata contro la guida nel vertice dell'anello sia uguale al suo peso.

 

 

ESERCITAZIONE n°5 (05/11/2015)

1.      Un autocarro di massa 2100 kg che viaggia verso nord alla ve­locità di 41 km/h svolta verso est e accelera fino a 51 km/h, (a) Qual è la variazione di energia cinetica del veicolo? Quali sono (b) il modulo e (e) la direzione della variazione della sua quantità di moto?

 

2.      Una caldaia esplode, rompendosi in tre pezzi. Due di questi, di uguale massa, partono, in direzioni fra loro perpendicolari e in versi opposti agli assi coordinati, alla stessa velocità di 30 m/s. Il terzo pezzo ha massa tripla di ciascuno degli altri due. Quali sono (a) modulo e (b) direzione della sua velocità immediatamente dopo l'esplosione?

 

3.      Una massa m = 2 Kg si muove verso destra con velocità v = 9 m/s e urta una massa M = 4 Kg che è immobile. Il piano su cui appoggiano è senza attrito. Studiare il sistema nel caso di urto completamente anelastico.

 

ESERCITAZIONE n°6 (17/11/2015)

 

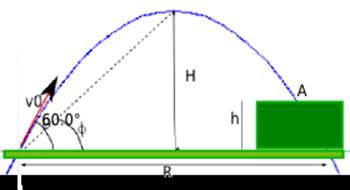
1)Una pietra viene proiettata verso un terrapieno di altezza h con la velocità iniziale di 42,0 m/s ad un angolo di 60° rispetto al suolo orizzontale (vedi figura). La pietra cade in A, 5,50 s dopo il lancio.        (a) Trovare l'altezza h del terrapieno;(b) la velocità della pietra subito prima dell'urto col terreno e la (c)massima altezza H sopra il suolo raggiunto dalla pietra.

 

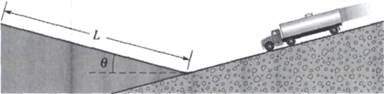
2) Un'autocisterna di massa , fuori controllo per un guasto ai freni, sta scendendo a precipizio alla velocità di 130km/h. Fortunatamente, vicino alla fine della discesa c'è una rampa di emergenza in contropendenza (priva però di attrito) con inclinazione θ=15°.(d) Quale deve essere la sua lunghezza minima per essere certi che riesca ad arrestare la cisterna? (e) La lunghezza minima aumenta, diminuisce o resta uguale se l'autocisterna ha massa minore? (f) e se la velocità è 2/3 di quella data?

 

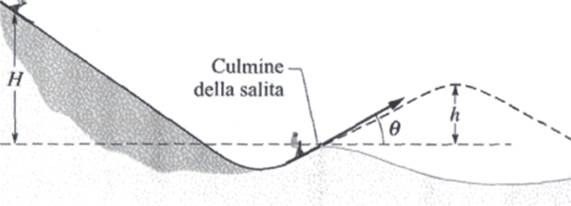
3) Uno sciatore di massa 60kg parte da fermo da un'altezza H=20m rispetto al culmine del trampolino di salto. Allo stacco dal trampolino la sua direzione forma un angolo θ=28° con il piano orizzontale. Trascuriamo l'attrito e la resistenza dell'aria. (g)Quanto varrà la massima altezza h raggiunta rispetto al punto di stacco? (h) Aumenta, diminuisce o resta invariata se lo sciatore ripete il salto con un pesante zaino?

 

 

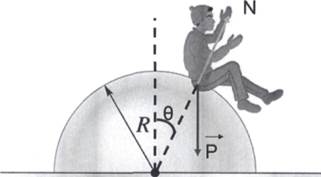
4) Un ragazzo è seduto sulla cima del blocco di ghiaccio semisferico di raggio R=13,8m della figura. Comincia a scivolare in giù con velocità trascurabile. (i) Se il ghiaccio è privo di attrito, a che altezza dal suolo si staccherà dal ghiaccio?Vedi figura.

 

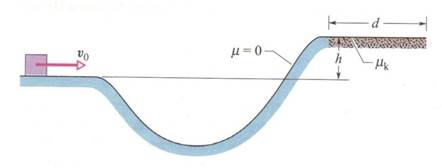
5) In figura vediamo un blocco che scivola lungo una pista da un livello a un altro livello più elevato, attraversando un avvallamento intermedio. La pista è priva di attrito fino a che si giunge al livello maggiore, dove invece esiste una forza di attrito che arresta il blocco dopo una distanza d.

(j) Trovate d sapendo che la velocità iniziale è v0=6,0m/s, la differenza di quota è h=1,1m e il coefficiente di attrito dinamico è ud=0,60.

 

 

 

 

 

 

 

ESERCITAZIONE n°7 (10/12/2015)

 

 

 

Settima esercitazione

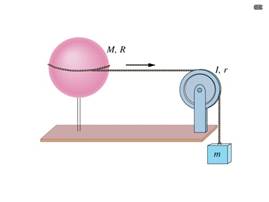
1.      Il guscio sferico uniforme in figura di massa M = 4,5 Kg e raggio R = 8,5 cm, ruota intorno ad un asse verticale su cuscinetti privi d’attrito. Una corda priva di massa avvolta intorno all’equatore della sfera, passando senza slittamenti sopra una puleggia, priva di attrito, avente momento d’inerzia      

 e raggio r = 5,0 cm, tiene appeso un piccolo oggetto di massa 0,60 Kg. La corda non slitta e il perno è privo d’attrito. Quale sarà la velocità dell’oggetto dopo che sarà disceso per una distanza h = 82 cm dalla posizione di riposo? Si considerino il lavoro e l’energia. 

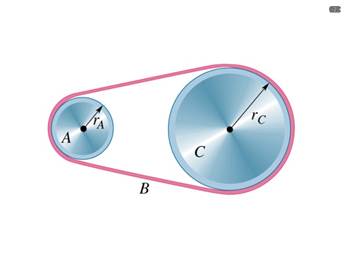
2.      La figura rappresenta lo schema di trasmissione a cinghia: la ruota A di raggio  è accoppiata tramite la cinghia B alla ruota C di raggio . La ruota A, partendo da ferma, aumenta la propria velocità angolare con accelerazione costante di 1,6 rad/s2. Calcolate quanto tempo impiega la ruota C per raggiungere la velocità angolare di 100 giri/min, ammettendo che la cinghia non slitti. (Suggerimento:  in assenza di slittamento le velocità lineari alla periferia delle ruote devono essere identiche. )

10.25

 

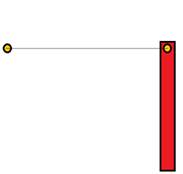
3.       Un oggetto sferico puntiforme  di massa m = 2 Kg che si sta muovendo alla velocità di 3 m/s urta un’ asta rigida e si conficca all’interno della stessa come in figura. L’asta ha la stessa massa della particella e lunghezza pari a 100 cm. Calcolare la velocità angolare della particella. 

 

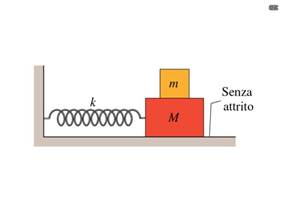
4.      Due blocchi (m= 1,0 kg ed M= 10 Kg ) e una molla ( k= 200 N/m ) sono sistemati come in figura su una superficie orizzontale priva d’attrito. Il coefficiente d’attrito statico tra i due blocchi è 0,40. Qual è la massima ampiezza del moto armonico semplice ammissibile per evitare lo slittamento tra i due blocchi?

15.24

 

ESERCITAZIONE n°8 (17/12/2015)

1.      Dati i seguenti due livelli sonori L1= 32 dB e L2= 54 dB individuare a quale intensità sonora corrispondono.

2.      Un osservatore si muove alla velocità di 48 m/s verso una sorgente ferma, che emette un suono di frequenza pari a 3 KHz. Determina la frequenza del suono udito dall’osservatore.

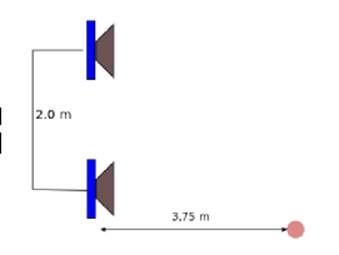
3.      Un osservatore è posto esattamente di fronte ad un altoparlante ad una distanza di 3,75 m. I due altoparlanti, che sono separati da una distanza D di 2,0 m , emettono toni puri di lunghezza d’onda λ.  All’uscita degli altoparlanti le onde sono in fase. Per quale lunghezza d’onda l’ascoltatore percepirà la minima intensità sonora?              E la massima intensità sonora?

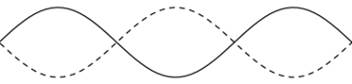
4.      Una corda di chitarra in nylon ha una densità lineare pari a 7,2 g/m ed è sottoposta ad una tensione di 150 N. I supporti distano 90,0 cm. La corda oscilla come lo schema di onda stazionaria mostrata in figura. Calcolare (a) la velocità, (b) la lunghezza d’onda e (c) la frequenza delle onde la cui sovrapposizione determina quest’onda stazionaria.

 

5.      Quanta energia è necessaria per scaldare 50g d’acqua da 20°C a 80°C? E se invece si trattasse di mercurio? (c H2O= 4190 J/ Kg K    c Hg= 138  J/Kg K)

 

 ESERCITAZIONE n°9 (--/--/2015)