Esercitazione Lunedì 11 Novembre 2013

CINEMATICA

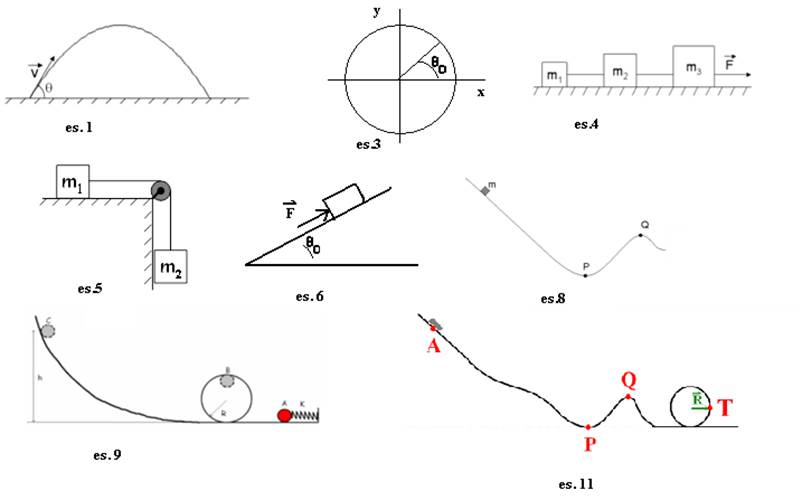
1) Una palla è lanciata in aria da terra (quota = 0 m). La velocità iniziale risulta essere, in modulo, v = 19,7 ^m/_s e forma un angolo

ϑ= 38,8° rispetto al piano orizzontale.

(a) Quale sarà l’altezza massima della palla?

(b) Quale sarà la distanza orizzontale percorsa?

(c) Quanto valgono le componenti del vettore velocità un istante prima che colpisca il terreno?

2) Una macchina frena dalla velocità di 25 m/s fino alla velocità di 12.5 m/s su una distanza di 100 m.

a) Se l’accelerazione è costante durante tutta la frenata, quanto vale l’accelerazione della macchina?

b) In quanto tempo avviene la frenata?

c) Se la macchina continua a frenare dopo quanto tempo si fermerà?

d) Se la macchina continua a frenare, quanta strada riuscirà ancora a percorrere prima di fermarsi ?

3) Una particella si muove di moto circolare uniforme. All’istante t₀ si trova nella posizione mostrata in figura. Sapendo che il raggio della circonferenza R è di 4,8 m che il modulo della velocità angolare w è di 1,3 rad/s e che ϑ₀ vale 1,1 rad determinare al tempo t = 2.7 s

a) la sua posizione angolare

b) le coordinate della sua posizione

c) il modulo della velocità lineare ( o tangenziale)

d) il modulo della accelerazione centripeta

DINAMICA

4) Tre blocchi collegati da due funi (come in figura) vengono tirati lungo una superficie priva di attrito da una forza orizzontale di 18 N. Sapendo che m₁ = 1kg, m₂ = 2kg e m₃ = 3 kg, determinare:

(a) Quale è l’accelerazione del sistema

(b) Quale è la tensione delle fune che collega m₁ a m₂

5) Un blocco di massa 5 kg è posto su una superficie orizzontale liscia ed è tirato da una fune attaccata a un blocco di massa 8 kg sospeso a una puleggia che ha soltanto lo scopo di cambiare la direzione della tensione della fune.

(a) Calcolare l’accelerazione del sistema

(b) Calcolare la tensione della fune

6) Un blocco di peso pari a 87 N viene appoggiato su un piano avente coefficiente di attrito statico μ_s = 0,25 e dinamico μ_d = 0,15 e inclinato di un angolo θ= 23° rispetto al piano orizzontale.

(a) Supponendo di applicare una forza esterna parallela al piano inclinato, quale deve essere l’intensità minima che deve avere per mantenere il blocco in equilibrio?

(b) Quale è l’intensità che deve avere la forza esterna per farlo muovere verso l’alto a velocità costante pari a 8 m/s?

CONSERVAZIONE ENERGIA

7) Un corpo è inizialmente fermo sulla sommità di un piano inclinato a una altezza di 10 m. Qual è la velocità del corpo quando raggiunge la base del piano inclinato (trascurando gli attriti)?

8) Un blocco di massa m = 8.6 kg parte da fermo su un piano inclinato da una quota h = 7 m. Il punto P si trova alla quota h = 0 m mentre il punto Q si trova a una quota pari a 1/3 della quota iniziale, come mostrato in figura:

Determinare:

a) L’energia cinetica nel punto P

b) L’energia meccanica nel punto Q

9) La pallina rossa in figura ha massa m = 50g e raggio trascurabile. Essa è poggiata ad una molla di costante elastica 500N/m nel punto A di una guida priva d’attrito.

Sapendo che la pallina nel punto A parte da ferma, che la molla è compressa di 10cm, e che il raggio del giro della morte è di 24cm, determinare:

(a) L’energia potenziale nel punto A in cui la molla è compressa di 10cm

(b) L’energia meccanica della pallina nel punto B

(c) L’altezza massima h raggiunta sulla guida dalla pallina

10) Un corpo è inizialmente fermo sulla sommità di un piano inclinato a una altezza di 10 m. Qual è la velocità del corpo quando raggiunge la base del piano inclinato (trascurando gli attriti)?

11) Una carrello di massa m = 2kg segue un percorso su binari articolato come in figura. Il carrello parte da fermo dal punto A ad un’altezza h = 20 m.

Trascurando gli attriti si determini:

c) L’energia cinetica nel punto P posto a quota h=0m

d) L’energia cinetica nel punto Q che si trova ad una quota pari ad 1/3 di quella iniziale

e) Sapendo che il raggio del giro della morte R è pari a 3,5m, si determini la reazione vincolare nel punto T, posto lungo la circonferenza, il cui raggio vettore R è parallelo all’orizzonte, come riportato nel disegno.

Esercitazione Mercoledì 27 Novembre 2013

Conservazione quantità di moto.

12) Un ragazzo di massa m₁ =70 kg è seduto su un carrello di massa m₂=35 kg che si muove in linea retta alla velocità di v=2,33 m/s. Il ragazzo salta in modo da atterrare a velocità nulla su la stessa retta su cui il carrello continua il suo moto.

Determinare la velocità finale v_f del carrello.

13) Due sfere di avorio si scontrano frontalmente. Il loro urto è elastico. La loro massa m=300 g, mentre le velocità sono rispettivamente di v₁= 2,5 m/s v₂= 1.8 m/s.  Determina le velocità successive all'urto

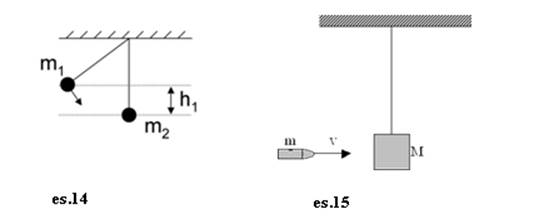
14) Due sfere sospese come in figura sono inizialmente a contatto. La sfera 1, con massa m1 = 57g, viene lasciata libera dopo essere stata tirata verso sinistra fino ad un’altezza h₁ = 13.5 cm. Ritornata, cadendo, nella posizione iniziale, subisce un urto elastico contro la sfera 2, di massa 73g. Qual è la velocità v_1,f della sfera 1 subito dopo l’urto?

15) Un blocco di legno di massa M = 5.4 Kg è sospeso a una fune. Un proiettile di massa m = 9.5 g è sparato contro il blocco, nel quale repentinamente si arresta. Il sistema blocco + proiettile oscilla quindi verso destra e il centro di massa del sistema si alza di una quantità h = 6.3 cm. Qual era la velocità del proiettile immediatamente prima della collisione?

Esercitazione Mercoledì 4 Dicembre 2013

1) Un lanciatore di martello scaglia il suo attrezzo dopo averlo fatto accelerare per 2,0 secondi, applicandogli una forza media di 35 N tangente alla traiettoria. Il martello pesa 2,5 Kg e la catena, di massa trascurabile, a cui è attaccato è lunga 90 cm.

Quanto vale il momento angolare del martello al momento del lancio?

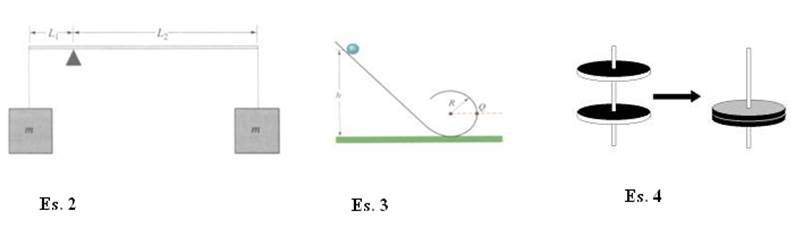
2) Due blocchi di uguale massa m sono sospesi alle estremità di una asticella rigida e priva di peso di lunghezza L1+L2, dove L1 = 20 cm e L2 = 80 cm. L’asticella è tenuta ferma sul fulcro nella posizione indicata in figura e quindi viene lasciata libera.

Calcolare l’accelerazione dei due blocchi nell’istante in cui cominciano a muoversi.

3) Una biglia omogenea di massa m e raggio r rotola senza strisciare lungo la pista rappresentata in figura essendo partita da ferma da un punto del tratto diritto della pista di lancio.

Da quale altezza minima h sopra il punto più basso deve partire per non staccarsi dalla pista alla sommità della gran volta (il raggio della gran volta è R >> r)?

4) Un disco gira solidale intorno a un albero, avente momento d’inerzia trascurabile, alla velocità angolare di 800 giri/min. Un’altro disco con lo stesso raggio ma momento d’inerzia doppio e inizialmente a riposo, è posto in contatto con il primo facendolo scivolare senza attrito sullo stesso albero.  Sapendo che il coefficiente d’attrito  tra I due dischi non è nullo:

Qual è la velocità angolare del sistema risultante albero + due dischi?

Esercitazione 11 Dicembre 2013

1) Un oggetto in moto armonico semplice impiega 0.25 s a spostarsi da un punto di inversione al successivo. La distanza fra questi due punti è 36 cm. Determinare :

· Il periodo del moto;

· La frequenza del moto;

· L’ampiezza del moto.

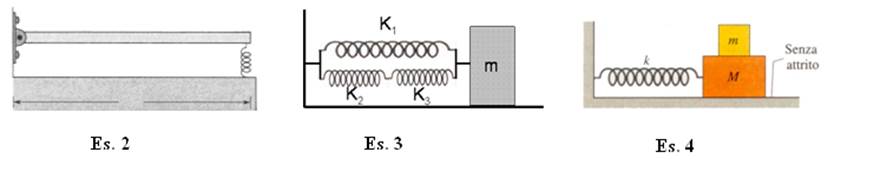
2)   Un asse di lunghezza L = 4.6 m e di massa M = 18 kg è incernierato a una parete sulla sinistra ed è sostenuto da una molla sulla destra, come mostrato in figura. Spostando di poco il sistema dalla sua posizione di equilibrio si generano delle oscillazioni semplici di piccola ampiezza. Supponendo che la molla abbia una costante elastica k = 2184 N/m e che la tavola sia perfettamente rigida, determinare:

· La pulsazione del moto armonico

· Il periodo di oscillazione del sistema.

3) Un blocco di massa m = 7.23 kg è collegato a una parete verticale tramite il sistema di molle mostrato in figura. Le costanti elastiche delle molle sono K₁ = 154 N/m, K₂ = 63 N/m, K₃ = 96 N/m. Determinare:

· La pulsazione del moto di oscillazione del sistema;

· L’accelerazione massima del blocco se la molla viene elongata di una quantità A=12 cm.

4) Due blocchi (m = 1.22 kg e M = 8.73 kg) e una molla (k = 344 N/m) sono posti su una superficie orizzontale senza attrito. Il coefficiente di attrito statico tra i due blocchi è 0.42. Trovare:

· La pulsazione del moto oscillatorio;

· L’ampiezza massima possibile del moto armonico semplice in assenza di scivolamento tra i due blocchi.

Esercitazione del 18 Dicembre 2013

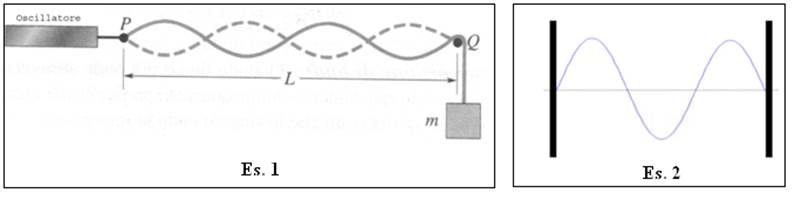
1) Una corda legata in P a un oscillatore sinusoidale e passante al di sopra di un supporto in Q è tesa da un blocco di massa m. La distanza L tra P e Q è 1.2 m, la densità di massa della corda è 1.6 g/m. L’ampiezza del movimento in P è abbastanza piccola da poter considerare questo punto un nodo. Un nodo esiste anche in Q. Se la massa vale 0.85 Kg, determinare:

a) La velocità dell’onda sulla corda tesa

b) La frequenza che deve avere l’oscillatore affinché sulla corda si instauri la quarta armonica?

2) Una fune di lunghezza L = 85 cm è fissata alle sue estremità a due pareti come mostrato in figura. La tensione della fune è pari a F = 180 N e la sua massa per unità di lunghezza è m = 12 g/cm. SI supponga che la fune oscilli nello stato corrispondente alla terza armonica e che la forma dell’onda mostrata in figura rappresenti l’onda nell’istante t = 0 s. Supponendo che in questo istante la sua elongazione sia massima:

a) Determinare la velocità dell’onda;

b) Determinare la frequenza dell’onda sonora emessa;

c) Rappresentare graficamente la forma dell’onda nell’istante t = ½ T (dove T è il periodo).

3) Una corda di violino è lunga 55.0 cm e pesa 440 mg. L’armonica fondamentale della corda ha una frequenza di 520 Hz. Si determini:

a) la velocità di propagazione dell’onda lungo la corda.

b) la tensione della corda.

c) la frequenza della terza armonica della corda.

d) la lunghezza d’onda del suono emesso nell’aria dalla corda nel caso c) (si assuma una velocità dell’onda sonora generata di 343 m/s )

4) Il livello sonoro medio di un ambiente di lavoro passa da 48 dB a 70 dB a causa di lavori di ristrutturazione. Determinare:

a) di quante volte è cresciuta l’intensità del suono a causa dei lavori

b) l’intensità del suono percepito durante i lavori

________________________________________________________________________

Esercitazione del 20 Dicembre 2013

1) Una lastra di superficie S = 4.5 m² è formata da due materiali a diretto contatto di spessore d₁ = 8 cm e d₂ = 9 cm aventi rispettivamente conducibilità termiche K₁ = 8.40 W/(m·K) e K₂ = 10.50 W/(m·K). Se le temperature costanti delle superfici esterne sono t₁ = 25 °C e t₂ = 18 °C calcolare la quantità di calore che attraversa la lastra nell’unità di tempo in regime stazionario.

2) Una sbarra cilindrica di argento, di sezione 4.76 cm² e lunghezza 1.17 m è isolata per impedire dispersioni di calore attraverso la superficie . Gli estremi sono tenuti a una differenza di temperatura di 100°C, uno in una miscela di acqua e ghiaccio e l’altro in acqua bollente. Se il calore latente di fusione del ghiaccio è di 3.33×10⁵J/kg si calcolino:

a) La quantità di calore trasferita nell’unità di tempo lungo la sbarra;

b) La velocità di fusione del ghiaccio all’estremo freddo.

3) Una macchina di Carnot lavora tra un serbatoio caldo a 332 K e uno freddo a 258 K. Se per ogni ciclo assorbe dal serbatoio caldo 586 J di calore:

a) Quanto lavoro produce ogni ciclo?

b) La stessa macchina funziona alla rovescia tra gli stessi serbatoi come un frigorifero. Quanto lavoro bisogna fornire in un ciclo per assorbire 1230 J di calore dal serbatoio più freddo?

4) Un salone viene mantenuto alla temperatura costante di 21° C, essendo la temperatura esterna è di 38° C, da una pompa di calore ideale. Se il calore viene dissipato in misura di 3.5 kW solo attraverso due pareti, aventi una estensione totale di 100 m² e spesse 25 cm, determinare:

a) Il coefficiente di prestazione della macchina frigorigena.

b) La conducibilità termica globale delle pareti.